Lesson 1: Factors and Multiples

Module 2: Roots and Powers

 

Watch and Listen

 

There are other methods of approaching GCF and LCM problems that do not involve prime factorization. The ladder method, for example, can be used to find the LCM and GCF of a set of two, three, or more numbers. Watch the video titled “Ladder Method” to see how this method is used.

Why Does the Ladder Method Work?

You might have seen from the beginning that 24 was the greatest common factor. Dividing both 72 and 120 by 24 would have resulted in 3 and 5, respectively. These last numbers can’t be divided further. Therefore, 6 × 4 is the greatest common factor.

In most cases though, you can also reach the same result by dividing the original numbers by smaller factors. The product of these factors would represent the largest divisor of the original numbers, or the greatest common factor.

In the video, the original numbers were divided by 6 and then by 4. At that point, no other common factors were available. The product of 6 and 4 is 24.

You could have also obtained the same result by dividing the original numbers by 2, then 2, then 2, then 3. Your work would look like this:

Notice here that the GCF is still 24 since 2 × 2 × 2 × 3 = 24.

Example 3

In this example you will learn how to use another method for finding the GCF and LCM of a set of numbers. This method involves listing all the factors and multiples of each number in the set until a match is found.

Consider the numbers 18, 24, and 30.

1. Find the GCF.
2. Find the LCM.

Solution

1. GCF
   Step 1: List the factors of each number in the set:
   

   • factors of 18 = 1, 2, 3, 6, 9, 18

   • factors of 24 = 1, 2, 3, 4, 6, 8,12, 24

   • factors of 30 = 1, 2, 3, 5, 6, 10, 15, 30

   Step 2: To find the GCF, find the largest factor common to all three lists. The answer is 6.

2. LCM
   Step 1: List the first few multiples of the largest number in the set:
   
   • multiples of 30 = 30, 60, 90, 120, 150, 180, 210, 240, 270, 300, 330, 360, 390

   Step 2: Choose the lowest multiple of 30 that is also a multiple of 18 and 24:

   • 18 divides into 90, 180, 270, 360, . . .
   • 24 divides into 120, 240, 360, . . .

   The LCM of 18, 24, and 30 is 360.

Try This 3

 

You have learned several methods for determining the GCF and the LCM of a set of numbers. These include prime factorization, the ladder method, and the method of listing factors and multiples. Which method do you prefer?

Practise using each of these methods to solve some basic problems. You may find that one method works better for you than another, but don’t let that stop you from trying the other methods, too!
Please complete the following exercises in your course folder (binder).

TT 3. Complete “Exercises” questions 8.c, 9.a, c, 10.c, 10.d, 11.a, c, 12 and 13 on page 140.

Use the link below to check your work.

Possible TT3 ( Try This 3 Solutions)

 

Self-Check

 

SC 1. Categorize the following numbers as prime, composite, or neither:

0, 1, 2, 93, 97, 2448

SC 2. Find the GCF for 60 and 75. Explain your reasoning.

SC 3. Find the LCM for 60 and 75. Explain your reasoning.

Compare your answers.

Finding the GCF and the LCM of numbers can be applied to problem-solving situations. Many problems are multi-step and require some type of plan. An effective way to approach a multi-step problem is to break the problem into smaller steps. This approach is similar to factoring large numbers. Just as you can more readily identify the GCF and LCM of numbers once they have been factored, you can solve a problem more effectively by dividing it into several smaller objectives.

 There are many things you need to do when solving problems. Ask yourself exactly what the problem requires. Then determine all the information being given to you in the question. Some key questions to ask include the following:

• What are the key words in the problem?
• Do I need a diagram? A list? A table?
• Is there a formula or equation that I will need? Which one?
• Is there a pattern I can use and/or follow?
• Can I break this problem into a few simpler problems?

As you work through problems, the following chart may help you organize your thinking:

 

Read the Problem	Explore	Select a Strategy	Solve	Look Back
Note key words. What is known? What is unknown? What are you asked to find? Restate the problem.	Organize the information. Picture the problem. Draw a diagram or table. Do you know a related problem that could help?	Here are just a few: pattern recognition working backwards guess and check reduce or simplify	Carry out your strategy.	Check your answer(s). Does it make sense?

 

The following example demonstrates how the steps in the chart can be used to approach a problem.

 Example 4

 

Two buses leave the terminal at 8:00 a.m. Bus A takes 90 minutes to complete its route; bus B takes 75 minutes. When is the next time the two buses will arrive together at the terminal (if they are on time)?

 Solution

 Read the problem:

 

Note key words. What is known?

• Bus A takes 90 minutes.
• Bus B takes 75 minutes.

What is unknown? What are you asked to find?

• You need to find out the time when the buses will both be back at the terminal together.

Restate the problem.

• What time will it be when both buses are back at the terminal?

Explore:

Organize the information. Picture the problem. Draw a diagram or table.

In this case, you are working with multiples, so a table makes sense.

Bus A	90	180	270	360	450	540	630
Bus B	75	150	225	300	375	450	525

 Select a strategy:

 Here are just a few: pattern recognition, working backwards, guess and check, and reduce or simplify.

For this question, you could use pattern recognition based on the table or you could use prime factorization.

Solve:

Carry out your strategy.

• Method 1: In the table, you can see that after 450 minutes, both Bus A and Bus B will be back at the terminal.
• Method 2: Alternatively, you might choose to use an algebraic method to solve this problem. In this case, you would use one of the strategies learned in this lesson to determine the LCM of 90 and 75.
  
   
  90 = 10 × 9
  
   
      = 2 × 5 × 3 × 3
  
   
      = 2 × 3 × 3 × 5
  
   
  75 = 3 × 25
  
   
      = 3 × 5 × 5
  Here, the LCM would include all the factors of 90 and those factors of 75 that have not already been taken into account with 90.
  LCM = (2 × 3 × 3 × 5) × 5
        = 450
  

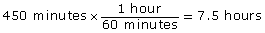
Look back:

Check your answer(s). Does it make sense?

Yes, it seems to make sense. However, the question asks for the time, not the number of hours before the buses meet back at the terminal. If the buses leave at 8:00 a.m., 7.5 hours after 8:00 a.m. is 3:30 p.m. Therefore, the buses will meet at 3:30 p.m.

Read

Work through an additional example where you can determine the GCF and LCM of a set of numbers to solve a problem.

 

Self-Check

SC 4. What is the side length of the smallest square that could be tiled with rectangles that measure 12 cm × 32 cm? Assume the rectangles cannot be cut. Sketch the square and rectangles.

 SC 5. What is the side length of the largest square that could be used to tile a rectangle that measures 12 cm × 32 cm? Assume the squares cannot be cut. Sketch the rectangle and squares.

Compare your answers.

 

Mathematics 10C Learn EveryWare © 2010 Alberta Education