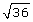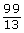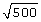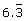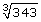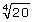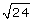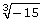Lesson 3: Irrational Numbers
Module 2: Roots and Powers
Watch and Listen
Retrieve your work from Try This 1 - 4. Did you learn that the prime factorization of a perfect square would always result in an even number of prime factors? Confirm this statement by looking at your results and conclusion. For example, the prime factorization of 144 is
144 = 2 × 2 × 2 × 2 × 3 × 3
The number 144 has six prime factors—an even number of factors—in its prime factorization.
An integer will have either an odd number or an even number of prime factors.
A perfect square will have twice as many prime factors in its prime factorization compared to its square root. Since you will always get an even number when you double any number, whether odd or even, a perfect square will always have an even number of factors in its prime factorization.
View the video titled “Root 2 Proof” to see how you can use this discovery to prove that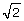 
is irrational.
The video shows just one way you can prove 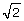is irrational. Generally, the square root of a number that is not a perfect square is irrational.
Similarly, the cube root of a number that is not a perfect cube is irrational.
Use the “Real Numbers” applet to review the differences between rational and irrational numbers. Study the nested diagram of Number Systems carefully and pay special attention to the examples given for both sets of numbers. You will need to recall this diagram later in the lesson.
So far in this lesson, you have learned that a rational number can always be written in the form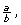 
where a and b are integers 
In decimal form a rational number is either terminating or repeating.
An irrational number cannot be expressed in the form 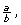where a and b are integers
In decimal form an irrational number neither terminates nor repeats. Rather, an irrational number continues indefinitely with no periodic pattern in its digits.
The non-terminating and non-repeating nature of irrational numbers makes it ideally suited for code construction. If you have constructed a code that requires a key or password to access, you can use a sequence of digits from an irrational number. Better yet, you can multiply two irrational numbers together to get a third irrational number and use any sequence of digits of that number as your key. If your code is intercepted, the only way it can be broken is if the intruder knows the two irrational numbers and also knows which sequence of digits to look for. Otherwise, the key looks just like a series of patternless digits!
Self-Check
SC 1. Classify the numbers as rational numbers or irrational numbers. Give your reasons for the classification.
|
Number |
Rational/Irrational |
Reason |
|
0 |
||
|
|
||
|
|
||
|
− 4.2558 |
||
|
− 4.2558 . . . |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
Now that you have determined how to identify irrational numbers, you can investigate how to locate irrational numbers on a number line. There are many strategies for doing this, with each strategy having its own advantages and drawbacks.
For example, one of the easiest ways to locate an irrational number on a number line is by using a calculator. However, a calculator can only give you an approximation of where a root might be located. As you read the next example, consider the advantages and drawbacks of each method.
Example 1
Use different strategies to locate the number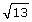 
on a number line.
Method 1: Calculator
Step 1: Evaluate
Step 2: Draw a number line.
Step 3: Insert the irrational number on the number line.
Since 
is slightly more than halfway between 3 and 4, it looks like this:
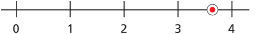
Method 2: Approximation Using Benchmarks
Think about the first few perfect squares:
|
Natural Number |
Square |
|
1 |
1 |
|
2 |
4 |
|
3 |
9 |
|
4 |
16 |
These numbers can be used as benchmarks to help you obtain a more accurate estimate.
Since 9 < 13 < 16, then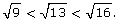 
In other words,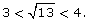 
Since 13 is a little closer to 16 than it is to 9, you can reason that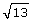 
is closer to 4 than it is to 3. A good guess might be 3.6 or 3.7.
Draw a number line with the point at approximately 3.6 (or 3.7).
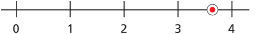
Method 3: Using a Compass and Straightedge
Watch and Listen
You can locate an irrational number more accurately with a compass and straightedge. Watch "Root 13 Construction" to see how this can be done.
Try This 5
TT 5. Complete the following questions in your course folder ( binder).
1. a. Compare and contrast the three methods used to locate an irrational number on the number line. Organize your ideas in the table.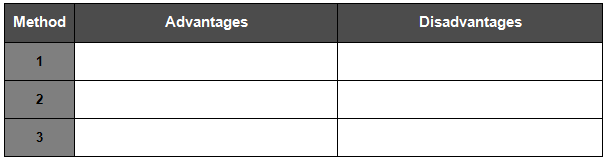
b. Which method do you prefer? Give your reasons.
c. In what situations would you use each method? In what situations would each method be inappropriate?
d. What other methods could be used to locate an irrational number on the number line?
Share
Compare your answers with another classmate or appropriate partner ( if possible). Record any similarities and differences you discussed in your course folder (binder).
Did You Know?
One form of high-level encryption depends on an unlimited source of patternless digits. This is an innovative application of irrational numbers.
Self-Check
SC 2. Place the following irrational numbers on a number line:
SC 3. Use the methods of locating irrational numbers to arrange the following irrational numbers on a number line:
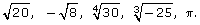
Try This 6
Complete the questions from your textbook in your course folder ( binder) to help you identify rational and irrational numbers and place them on a number line. Use your calculator to check that your result is accurate.
Foundations and Pre-calculus Mathematics 10 (Pearson)
TT 6. Complete “Exercises” questions 3 and 12 on page 211.
Use the link below to check your answers to Try This 6.