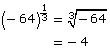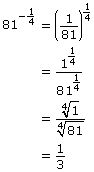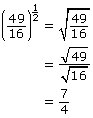Lesson 6: Rational Exponents

Math 10C Module 2 Lesson 6

Module 2: Roots and Powers

Explore

This shows a photo of a student writing the solution to a math problem on the whiteboard.

When you are learning to speak a new language, it is natural to continue thinking in terms of your native tongue and then translating it into the words of the new language. Similarly, when someone speaks to you in the new language, you will take a moment to translate what has been said into English before responding.

In this lesson you will explore how powers with rational exponents are like a new language for those who already understand radicals—the native tongue. You will convert between rational exponents and radicals.

Glossary Terms

Add the following term to your "Glossary terms":

rational exponents

-----------------------------------------------------

You saw in Math Lab: Powers and Radicals that powers with rational exponents are related to radicals. For example, you likely noticed that The pattern you discovered follows the rule where n is a natural number.

Tips

Another way to make the connection between powers with rational exponents and radicals is to think that since

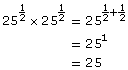
and

Therefore,

There are restrictions on the value of the radicand a depending on whether the value of n is even or odd.

Since a negative number cannot be square rooted to give a real solution, the value of a must be positive when n, the index, is equal to 2. This is because neither a negative number nor a positive number can be squared to give a result that is negative. In fact, it is not possible to multiply an even number of like factors together to give a negative product.

For example, 3 × 3 = +9 and (−3) × (−3) = +9, but there is not a number that can be squared to give −9. It is true that 3 × (−3) = −9, but that is not squaring since 3 and –3 are not the same number.

Therefore, when the value of n is even, a must be positive. When the value of n is odd, the value of a can be positive or negative.

Example 1

Use the pattern you discovered to evaluate the following powers.

Solution

Caution

It is important to pay attention to the placement of brackets when working with exponents. There is a difference between

In the first case, the base is −9

that has no real solution.

In the second case, the base is 9. The negative is not part of the base since there are no brackets to indicate this. Therefore,

eqn181.eps

You are now able to compute powers where the exponent is a fraction of the form What about rational exponents of the form The following example will show how you can change powers with any rational exponent into an equivalent radical.

Example 2

Evaluate

Solution

Method 1

Method 2