Lesson 6: Rational Exponents

Module 2: Roots and Powers

 

Share

Compare your answers to the following questions with another classmate or appropriate partner ( if possible). Record any similarities and differences you discussed in your course folder (binder).

Answer the following questions:

  1.   Describe the differences between method 1 and method 2 as shown in Example 2.     

  2.   List at least one advantage for each method. Which method do you prefer? Use the link provided to check your answers.

Answers

You can see that since both result in the same answer: 64.

This leads to the rule

where suggests you evaluate the nth root first and then apply the exponent m and suggests you apply the exponent m first and then evaluate the nth root. You will get the correct answer in either case.

 

Read

Go to the textbook and work through the following examples. Is there a quick way to remember how to convert a power into a radical, and vice versa? As well, pay attention to how decimals, negative bases, and negative exponents are treated.

 

Self-Check

These questions are based on the examples you just read. There may be more than one way of solving these questions. If your method does not match the one provided, check with your teacher to confirm whether your method is appropriate.

Go to the textbook.

Compare your answers.

 

Try This 1 and 2

Complete the following in your course folder ( binder).

Foundations and Pre-calculus Mathematics 10 (Pearson)

TT 1. Complete “Exercises” questions 4.b, 6.b, 7.e, 9, 10.c, 11.e, 12.f, 13.c, 15, and 19  on page 227 and 228.
TT 2. Complete the following “Exercises” questions 10.a, 10.d, 10.f, 10.g, 15.b, 15.d and 16.c., 16.d on page 242 and 243.
Use the link below to check your answers to Try This 1 and 2.

Possible TT1 and 2 Solutions

 

You have now learned a total of eight exponent laws! These include the first five you learned in your previous math courses, as well as the newly learned zero exponent, integral exponent, and rational exponent laws.

How do you know if you have the right answer to a question? If you have completed multiple steps to arrive at the final answer, how do you know you didn’t make a mistake in one of those steps?

When confronted with the task of simplifying an expression involving exponents, you will likely have to apply several of these laws. You will have the freedom to approach the problem in several different (and correct) ways. However, because these problems involve multiple steps, you are at risk to make an error. Examples of errors could include forgetting to reciprocate a base or forgetting to include the negative sign with a base when it is not appropriate to do so.

A simple way to know is to enter the original expression into your calculator and then enter the final answer into the calculator. Compare those results to see if they are the same. If they are not, and you have entered both numbers in a correct manner, then you should check your work for errors. If they are equal, then you have used a correct method!

Identifying Errors

In the last section of this lesson you will analyze some typical student work that contains such errors. Can you detect the errors and, given the chance, advise the student as to how to correct the work?

Example 3

In the following solution, identify the error that was made.

Step 1: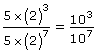

Step 2:

Step 3:

Step 4:

Step 5:

Solution

The sequence from step 2 to step 5 is correct. Starting with the quotient law is used to get 10– 4 in step 3. Then the Integral Exponent Law is applied to get the final answer. The error, however, is in the very first step; that is, and The student multiplied the 5 to the base 2, but that is incorrect because according to the order of operations, exponents should be treated before multiplication.

A correct approach would be to deal with the coefficients separately. So,

 

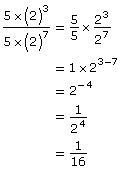
Try This 3 and 4

For practice, here are a few error-identification questions. Be sure to identify not only the incorrect work but also explain why the work is incorrect. Then provide the correct solution.
Complete the following in your course folder ( binder).

Foundations and Pre-calculus Mathematics 10 (Pearson)

TT 3. Complete “Exercises” questions 18 and 22 on page 228.

TT 4. Complete “Exercises” questions 17.a) and 19 on page 242.

Use the link below to check your answers to Try This 3 and 4.
Possible TT 3 and 4 Solutions

 

Mathematics 10C Learn EveryWare © 2010 Alberta Education