Lesson 1: Multiplying Binomials

Math 10C Module 2 Lesson 6

Module 3: Polynomials

Lesson 1 Summary

In this lesson you investigated the following questions:

How is multiplying binomials similar to multiplying two-digit numbers?
How is the process of multiplying binomials similar to encoding a message?

You examined two strategies that can be used to multiply binomials. One method was the area method using algebra tiles. This method models the multiplication of two binomials by relating the side lengths of the tiles to the area of a rectangle. Using algebra tiles helps you to visualize the problem.

The second method, the distributive property, is based on the idea that each term of one binomial is multiplied to each term of another binomial. In this respect, multiplying binomials is similar to multiplying a pair of two-digit numbers. You learned this by breaking each two-digit number into tens and ones and then placing those numbers in a multiplication array. In the same way as you would for a binomial multiplication, the product of each row and column are added together to obtain the final result.

You also learned that the acronym FOIL is a way to remember how to apply the distributive property to binomial multiplication.

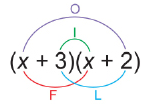
This shows an illustration of how to use the acronym FOIL to multiply binomials together.

No matter which method you use to multiply binomials, there is an algorithm or procedure that you must follow to obtain the correct answer. Likewise, when you are encoding a message, you must follow a particular procedure to obtain the correct ciphertext. Another similarity between multiplying binomials and encrypting messages is the fact that the plaintext and ciphertext look significantly different from each other.

In subsequent lessons you will learn about another common property to polynomials and secret codes. That is, they both can be reversed. Polynomials can be factored to recover the original binomials, and ciphertexts can be deciphered to recover the original message.

In the next lesson you will continue to explore the use of the distributive property to multiply polynomials. You will also discover a way to verify that you have obtained the correct product by substituting numerical values.