Print this chapterPrint this chapter

Lesson 4: Factoring Trinomials of the Form ax^2 + bx + c

Math 10C Module 3 Lesson 4

Module 3: Polynomials

 

Connect

In this lesson you learned strategies that can be used to factor trinomials of the form ax2 + bx + c. Take the opportunity now to update your Factoring Strategies document ( This should have been saved from Lesson 3 or copied by hand). Add information to your document that will help you to remember the steps of each method. Also, add notes that will help you recognize which strategy to use in a given situation.

In the final Try This section of this lesson, you examined ways in which errors can be made in the factoring of a polynomial. You may have noticed some errors in your classmates’ work as well as your own. It is a good idea to include notes about such errors in your chart as a reminder of how to avoid these types of error.

As you continue to learn new strategies for factoring different types of polynomials, continue to add to this chart. By the end of this module, you will have an invaluable study tool that can help you review some of the major outcomes you have learned.

m10c_refcon.jpg Lesson Assessment

Complete the lesson quiz posted under the Assess tab or by using the Quizzes link under the Activities block. Also, ensure your work in your binder (course folder) is complete. 

----------------------------------------------------------------------------------------


m10c_projcon.jpg Project Connection ** NOT ASSIGNED**

The following photo shows the Navajo Code Talker monument in Window Rock, Arizona, USA. This photo is a clue to the Project Connection for this lesson.

This shows a photo of the Navajo Code Talker monument in Window Rock, Arizona, USA.

You can use trinomial factoring as the basis of a cipher. Go to the Unit 2 Project. Complete the Module 3: Lesson 4 portion of the project to decipher the names of two actors who starred in a movie about secret codes. Use their names as keywords in your search engine to discover the name of the movie.

m10c_gb.jpg Going Beyond

In the Going Beyond section of the previous lesson, you learned how to use a graphing calculator to verify the factors of a polynomial. Now you will investigate how the graph of a trinomial of the form ax2 + bx + c can help you to identify its factors.

Factor the trinomial x2 + 2x – 15.

On a graphing calculator, complete the following steps.

Step 1: Enter Y1 = x2 + 2x – 15.

This shows a screenshot of a graphing calculator with the trinomial x2 + 2x - 15 entered into the Y = editor.

Step 2: Execute the Graph command. This type of graph is called a parabola.

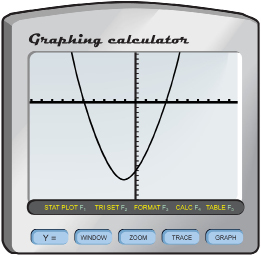
This shows a screenshot of a graphing calculator displaying the graph of the trinomial x2 + 2x - 15.

Step 3: Determine the points on the graph where the parabola intersects the horizontal axis. These are called the x-intercepts.

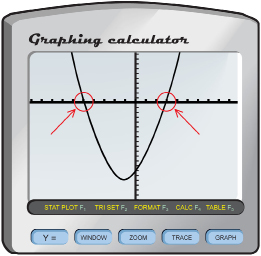
This shows a screenshot of a graphing calculator displaying the graph of the trinomial x² + 2x - 15. The x-intercepts are indicated in red.

Answer the following questions. You should save your answers to your course folder. Also, check with your teacher to see if you are required to submit the answers to these questions for marks.

  1. How do the x-intercepts compare with the coefficients of the binomial factors of x2 + 2x – 15?

  2. Repeat steps 1 and 2 using the trinomial 2x2 + 15x + 7. How do the x-intercepts compare with the coefficients of the binomial factors of 2x2 + 15x + 7?

  3. Graph the following trinomials. Try to determine the factors of each trinomial by looking only at the graph.

    1. x2 – 6x + 5
    2. 2x2 – 13x + 6

Share the answers to the questions with a partner. Find out how your partner responded to the questions and also if he or she noticed the same results as you did.

You will have the opportunity to further explore this relationship between a graph and a trinomial in future math courses.