Lesson 4: Factoring Trinomials of the Form ax^2 + bx + c

Method 4: Factoring by Inspection

Another way of factoring trinomials is by inspection. This method is based on reasoning and educated guesswork. This method can be done quickly as long as the coefficients are relatively small and have few factors.

The method of inspection is based on a consideration of the factors of the x²-term and the constant. Through trial and error, factors are accepted or rejected. As a result, it is important to check your final answer by multiplying the factors to see if the trinomial is recovered.

Watch and Listen

Watch the video titled “Factoring by Inspection” to see a demonstration of how to use the method of inspection to factor the trinomial 2x² - 7x + 6. Pay careful attention to how the coefficients of the trinomial are used to determine the coefficients of the binomial.

Read

The following example show how to complete a factoring question by Inspection or by "Using logical Reasoning".

Foundations and Pre-Calculus Mathematics 10( Pearson)
Read " Example 3: Factoring a Trinomial Using Logical Reasoning on page 172 - 173.

Try This 3

Practice applying the method of Inspection or Logical reasoning to the questions below.
Why would this process be appropriate for these questions?

Factor using inspection and then verify by multiplying
1. 2m² + 3m - 9
2. 12y² + y - 1
3. 2x² - x - 1
4. 3x² + x - 2

Possible TT3 ( Try This 3) Solutions

Common Errors

As you practice factoring using the methods that you have learned in this lesson, you should be aware of some common errors that can occur. Some of these errors are due to inattention to details but do not imply student misunderstanding. Other types of errors reveal a misconception of the recently learned math principles.

The following examples show how a student may factor a polynomial using the methods learned in this lesson.

Self-Check

SC 4. Study the solutions and identify the error that has been committed. Then correct the error and complete the solution.

Factor 2x² + 7x + 6. Find two numbers whose product is 6 and whose sum is 7. The numbers are 6 and 1.
Therefore, the binomial factors are (x + 6)(x + 1).
Since the leading coefficient is 2, the final factored form is 2(x + 6)(x + 1).
Factor 6x² + 11x – 10. Find two numbers whose product is –60 and whose sum is 11.
The two numbers are 15 and –4.
Set up the tic-tac-toe grid.

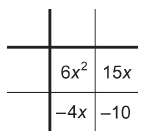
Determine the GCF for each column of terms and row of terms.

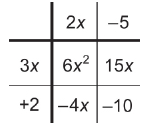
The factors are (2x – 5)(3x + 2).

Compare your answers.

Try This 4

Be sure to identify the error and also to correct it. As you examine the solutions, focus on this question: During what phase of a solution are errors usually found? Are the errors found in the initial steps, the last steps, or the intermediate steps?
Complete the following in your course folder ( binder) and use the link provided to check your work.
Foundations and Pre-calculus Mathematics 10 (Pearson)
Questions 16a and 17 on page 178

Possible TT4 ( Try This 4) Solutions