Lesson 5: Factoring Special Polynomials

Module 3: Polynomials

Explore

Glossary Terms

Add these terms to your "Glossary Terms' in your notes:

• conjugate binomials

• difference of squares

• perfect square trinomial

--------------------------------------------------------------------

 

Factoring a Difference of Squares

 

A special case of a trinomial is known as a difference of squares. You will recognize a polynomial as a difference of squares when you observe that the polynomial

• is a binomial

• has a first term that is a perfect square

• has a second term that is a perfect square

• shows the subtraction of one term from another

As an example, x2 – 4 is considered a difference of squares since both x2 and 4 are perfect squares and one is being subtracted from the other. Although x2 – 4 is expressed as a binomial, it can be viewed as a trinomial whose x-term has a coefficient of zero. In other words,

x2 – 4 = x2 + 0x – 4

When viewed this way, a difference of squares can be factored by using trinomial factoring methods. In this case, you can use the product-sum method.

Example 1

Factor x2 – 4.

Solution

Think about the difference of squares as the trinomial x2 + 0x – 4.

Step 1: Find two numbers whose product equals –4 and whose sum equals 0.

First Number	Second Number	Product	Sum
1	–4	–4	–3
2	–2	–4	0

Choose the combination that gives the correct sum. (See the numbers shown in the second row of the chart.)

Step 2: Express the polynomial as a product of its factors.

x2 – 4 = (x + 2)(x – 2)

Do you notice that the two factors are almost identical except for the sign of the constant? These factors are known as conjugate binomials.

 

 

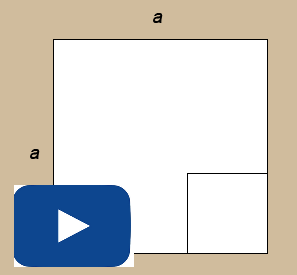
There is another method of factoring a difference of squares. In the Discover section you used graph paper to visualize a difference of squares by removing a square with smaller dimensions from one with larger dimensions.

Retrieve and review your Math Lab results. Compare the last three columns of your completed table to the one below.

Dimensions of Original Square	Dimensions of Removed Square	Rectangle Length	Rectangle Width	Rectangle Area
10 × 10	6 × 6	10 + 6	10 – 6	(10 + 6)(10 – 6)
8 × 8	3 × 3	8 + 3	8 – 3	(8 + 3)(8 – 3)
7 × 7	4 × 4	7 + 4	7 – 4	(7 + 4)(7 – 4)
5 × 5	2 × 2	5 + 2	5 – 2	(5 + 2)(5 – 2)

Can you see how the area of the rectangle can be determined by knowing only the dimensions of the original square and the removed square?

Watch and Listen

Watch the video titled “Difference of Squares” to see how this pattern can be generalized for any square.

Example 2

Factor 9x2 – 4y2 completely and check by multiplying.

Solution

Step 1: Determine the square roots of 9x2 and 4y2.

Step 2: Write one factor as the sum of the square roots. Write the other factors as the difference of the square roots.

9x2 – 4y2 = (3x + 2y)(3x – 2y)

Step 3: Check by multiplying.

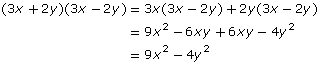
The original difference of squares is recovered, so the factors are correct.

Example 3

Factor 2m4 – 162 completely and check by multiplying.

Solution

Step 1: Check for common factors.

The greatest common factor is 2.

Therefore, 2m4 – 162 = 2(m4 – 81).

Step 2: See if you can continue to factor the binomial.

You can continue to factor m4 – 81 as a difference of squares.

Determine the square roots of each term in the difference of squares.

Therefore, 2(m4 – 81) = 2(m2 + 9)(m2 – 9).

Step 3: See if you can continue to factor the binomials.

You can continue to factor the binomial m2 – 9 as a difference of squares.

m2 = m × m

 9 = 3 × 3

 So, 2(m2 + 9)(m2 – 9) = 2(m2 + 9)(m + 3)(m – 3).

 

 

Step 4: Check by multiplying.

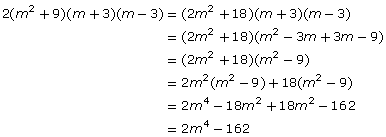
The original difference of squares is recovered, so the factors are correct.

Watch and Listen

You have just learned two ways to approach the factoring of a difference of squares. If you feel that you would benefit from another explanation, go to the YouTube website  “Mathcast 014 Using Algebraic Patterning to Factor a Difference of Squares” video.

Read

In your textbook, there are some additional examples of factoring a difference of squares using the ideas developed in this lesson. As you read, check that the polynomials meet the conditions for factoring as a difference of squares.

 

 

Self-Check

SC 1. For each of the following questions, decide if the expression can be factored as a difference of squares. If so, factor the expression completely. If not, explain why it cannot be factored.

1. x2 + 4
2. –9x2 + 36y2
3. –x2 – 49
4. 81x2 – 144y2

Compare your answers.

Try This 1

 

Apply the method of factoring a difference of squares to these questions from your textbook. Remember that certain conditions have to be met before this technique can be used to factor a polynomial. You may want to review these conditions before you attempt these questions.

Complete the following in your course folder ( binder).

Foundations and Pre-calculus Mathematics 10 (Pearson)

TT 1. Complete “Exercises” questions 6.b), 6.d), 10.a), 10.c), 10.e), 10.g), and 21 on pages 194 and 195.

Use the link below to check your answers to Try This 1.

Possible TT1 (Try This 1) Solutions

 

Mathematics 10C Learn EveryWare © 2010 Alberta Education