Lesson 4: Slope

Math 10C Module 4

Module 4: General Relations

Explore

In a cold northern climate where the snowfall is heavy, it’s best to have a roof with a steep pitch so that the roof will shed the snow and rain as thoroughly as possible. In a warm southern climate where there is no snow and where the rain fall is not large, a flat roof may be safely used and will be more economical to construct.

This shows a photo collage of two homes—one with a steep roof and one with a flat roof.

In this lesson you will explore slope. Slope is used to describe the steepness of any feature such as a hill, stream, road, staircase, ramp, or roof.

Glossary Terms

Add the following terms to your "Glossary terms" section in your notes. You may also want to add examples that demonstrate how each term is applied.

rise
run
slope

-----------------------------------------------------------------------

In mathematics, SLOPE is the ratio of the vertical change to horizontal change or rise over run.

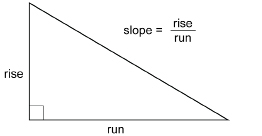
This shows an illustration of a right triangle. The vertical length or height of the triangle is labelled the rise, and the horizontal length or base of the triangle is labelled the run.

The vertical change is called the rise. The horizontal change is called the run.

Watch and Listen

Watch the short video on “Slope as Rise Over Run.”

Try This

This shows a photo of a woman in a wheelchair who is moving up a ramp towards the door of a house.

Many buildings have ramps for people in wheelchairs. In TT 1, you will consider two ramps with different dimensions.

Read the following example to see how you can use the rise/run ratio to calculate the slope of each ramp in the TT 1. Compare this result with your prediction in the previous Try This activity.

Example 1

Many buildings have ramps for people in wheelchairs. The illustration below shows two ramps with different dimensions. Predict which ramp is steeper. Use the rise/run ratio to determine which ramp is steeper. Support your reasoning without using a calculator. Do your work in your course folder ( binder).

Possible TT 1 Solution

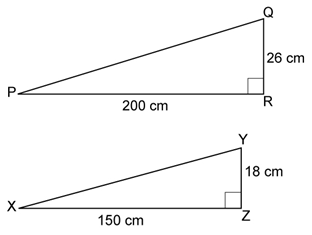
Step 1: Determine the slope of each ramp.

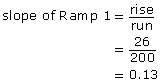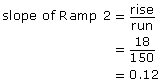The slope of Ramp 1 is 0.13. The slope of Ramp 2 is 0.12.

Step 2: Compare the slopes.

0.13 > 0.12

Ramp 1 has the steeper slope.

Try This 2 - 7

You will analyze a number of lines in a coordinate plane and compare these lines with respect to their slope.

Print and complete the following in your course folder ( binder).
Try This 2 - 7

Use the link below to check your answers to Try This 2 - 7.

Possible TT2 - 7 (Try This 2 - 7) Solutions

Watch and Listen

Watch the “Investigating Slope” video to see how you can use points to determine the rise and run of a line. After viewing the video, you will do another Try This Activity. Username LA53, password 4487.

Try This 8 - 10

As you worked through the examples of calculating the slopes of lines, did you see another possible way to find the rise and run?

Complete the following in your course folder ( binder).

TT 8. What if you wanted to start at a different point on the graph? Would it make a difference in the value of the slope? Why or why not?

TT 9. What if you started at a point that was higher up on the graph and counted down to the next point? Would that make a difference in the value of the slope? Why or why not?

TT 10. Suppose the slope is an integer. How do you identify the rise and the run?

Use the link below to check your answers to Try This 8 - 10.

Possible TT8 - 10 (Try This 8 - 10) Solutions

Self-Check

Now that you have seen a demonstration of how to calculate the slope of a line using two points on the line, you can apply what you have learned to the following exercise.

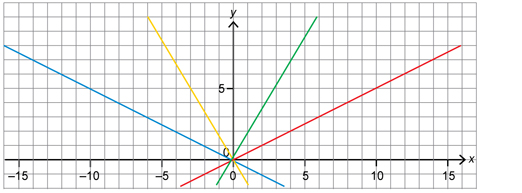
SC 1. Calculate the slope of the red and blue lines.

This shows a graph of four lines. Two lines rise from left to right. The other two lines are the reflections of the first two lines across the vertical axis.

Compare your answers.