Print this chapterPrint this chapter

Lesson 3: Slope Intercept Form

Math 10C Module 5: Lesson 3

Module 5: Linear Functions

Launch

This section checks to see if you have the prerequisite knowledge and skills to be able to complete this lesson successfully. 

Are You Ready?

Complete these questions in your course folder (binder). If you are experiencing difficulty, you may want to use the information and the multimedia in the Refresher section to clarify concepts before completing these exercises.

Lesson 3: Are You Ready?

Once you have completed these exercises to the best of your ability, use the provided answer link to check your work.
Answers
If you feel comfortable with the concepts covered in the questions, move forward to Discover. If you experienced difficulties or want more practice, use the resources in Refresher to review these important concepts before continuing through the lesson or contact your teacher.
** There is a nice solved example you SHOULD look at in the refresher section**

 

Refresher

The purpose of this section is to provide you with some resources to review in preparation for the lesson ahead. These resources may include videos, interactive applets, mini-lessons, and flash games to help you recall previously learned concepts. You can use these resources either before or after you try the Are You Ready? questions.Your teacher may also direct you to this section to review specific concepts.

-------------------------------------------------------------------------------------------

Review how to find the Slope of a Line and the intercepts from a graph.

-------------------------------------------------------------------------------------------

Review Module 4: Lesson 5: Example to see how you can graph a line given its slope and a point on the line.

 

Module 4: Lesson 5: Example

Example

A line passes through the point (−2, −5) and has a slope of 3.

  1. Determine two other points on the line.

  2. Sketch the line.

Solution

  1. To determine the rise and run of a slope of 3, write the slope as a fraction.

    Step 1: Determine the rise and run of the slope.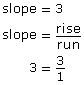

     


    Therefore, the rise is 3 and the run is 1.
    Step 2: Graph the point (−2, −5). Then apply a rise of 3 units up and a run of 1 unit to the right to find another point on the line. The second point will have coordinates (−1, −2).
    Since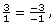 you could also apply a rise of −3 and a run of −1. In other words, you could also move down 3 units and left 1 unit.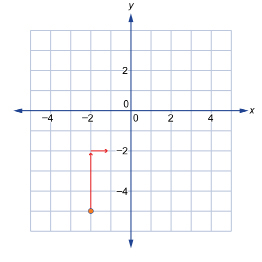

     

    This shows a graph of the point (-2, -5) with an arrow indicating a rise of 3 units up and another arrow indicating a run of 1 unit to the right of the arrow.
    Step 3: Since the slope of a line is constant, you can find additional points by applying the rise and the run to each new point. A third point found in this way is (0, 1).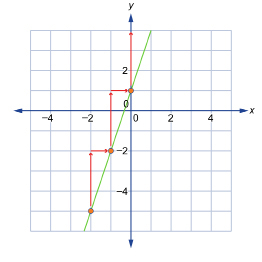

     

    This shows a graph of a line that passes through the points (−2, −5), (−1, −2), and (0, 1).

  2. Use a straightedge to connect the points on the graph with a line.

----------------------------------------------------------------------------------------------------

Lastly, go to “Formula” to review the definition of formula and how to rearrange formulas. In the Example section, you will see how the width variable in the perimeter formula can be isolated by balancing both sides of the formula. There is also a second example that shows how the radius variable in the circumference formula can be isolated.

 ------------------------------------------------------------------------------------------------------

If you would like a more thorough review in preparation for this lesson, refer to the Explore sections of the following lessons:

  • Module 4: Lesson 4

  • Module 4: Lesson 5

  • Module 5: Lesson 1