Lesson 4: General Form and Slope-Point Form

Module 5: Linear Functions

Explore

The marathon is a long-distance foot race. In the Olympics, the official distance of the marathon is 42.195 km (or 26 mi and 385 yards). The design of a marathon course depends on several factors. Many courses minimize the number of hills and tight corners in order to make it easier for the athletes to run fast times. The way that a course is designed may also be based on how convenient it is for spectators and television crews to view the race. Since the host city is different from one Olympics to the next, the marathon course is also different at each Olympics. The one thing that remains the same, however, is the distance.

In Lesson 3 you learned to describe a linear function using the slope-intercept form, y = mx + b. In this lesson you will learn about two other forms. While all of these forms are different in appearance, like the Olympic marathon courses, they can all be used to describe the same linear function!

Glossary Terms

 Add these terms and their definitions to your "Glossary Terms" section in your notes. You may also want to add examples that demonstrate how each term is applied.

• general form
• slope-point form
• standard form

-----------------------------------------------------------------------------------------------------------------------------------------

Slope-Point Form

In the last lesson you learned to construct the equation of a line using its slope and y-intercept. You can actually use any point on a line to construct the equation of a linear function.

 

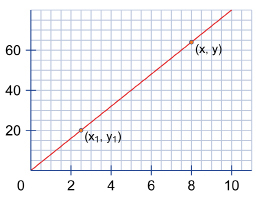
Recall the slope formula for determining the slope of a line with points at (x1, y1) and (x2, y2):

Examine the line in the slope-point form graph. If a line passes through the point (x₁, y₁), then you can take any other point on that line (x, y) to determine the equation of the line. You will do this by using the slope formula:

This form for the equation of a linear function is called slope-point form.

Read

The following example demonstrates how the equation of a linear function can be expressed in slope-point form. As you work through the example, focus on the order of the steps for converting an equation in slope-point form to slope-intercept form. 

 

Self-Check 3

 

SC 3. The graph of a line that passes through the point (8, 3) with a slope of is shown.

 

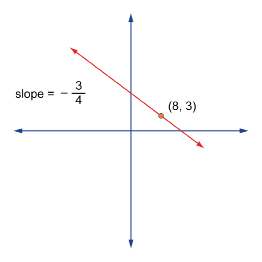
1. Write the equation of the line in slope-point form.
2. Convert the equation in part a. into slope-intercept form.

Compare your answers.

General Form

Another way to express the equation of a line is called general form. The general form of a graph is written as where A is a whole number, B and C are integers, and A and B cannot both be equal to zero.

KEY IDEA To ensure that an equation is in correct general form, make sure the coefficient in front of the x in positive and that none of the coefficients are fractions. To do this, multiply each side and each term by a number that changes the coefficients to match these restrictions. ex. If we have y = -1/2x + 6 and we want to change it to correct general form, there are two steps. Step 1: Move the y term to the right side and equate to 0. 0 = -1/2x - y + 6. Step 2: Multiply each term by -2 to get rid of the fraction and the negative in front of the x term. -2(0) = -2(-1/2x) -2(-y)+ -2(6) 0 = x + 2y -12 THIS IS CORRECT GENERAL FORM

Retrieve your tables from Math Lab: Linear Forms. Check the last column of each table for examples of linear functions written in general form. Compare the general form to the other forms of linear functions.
Think about the following questions:

1. In what ways is the general form different from the other forms? In what ways is the general form similar to the other forms?
2. What are the benefits of expressing a linear function in general form?
3. Select equations from the tables in Math Lab: Linear Forms to show how you can convert from
        a.   slope-intercept form to general form           
        b.   general form to slope-intercept form

 Possible Solutions are:

1. The general form has one side of the equation as 0; the other forms have x and y on opposite sides of the equal sign. The general form is similar in that its graph is also a line and it has x, y, and constant terms.
2. You can easily find two points to graph. The first point can be found by using x = 0 and solving for y; the second point can be found by using y = 0 and solving for x.
3. a.   Any slope-intercept form can be transformed to general form using these steps.

              y = mx + b
         y – y = mx + b – y  **Subtract y from both sides**
              0 = mx – y  + b ** We just change the letters to match general form
              0 = Ax + By + C ** if there are any fractions, we multiply every term by the
                                       lowest common denominator and if A is negative, we  
                                       multiply every term by -1**

            ex.   y = -1/2x + 5
              y - y = -1/2x + 5 – y
                   0 = -1/2x – y + 5  ** since the coefficient in front of x is a fraction AND is
                                               negative, we multiply every term by -2
              -2(0) = -2(-1/2x) – (-2)y + -2(5)
                    0 = x + 2y - 10

 b.   Any general form can be transformed into slope-intercept form using these steps.

                                    Ax + By + C = 0
                       Ax – Ax + By + C – C = 0 – Ax – C **Subtract the Ax and C to leave the By term on the left** 
                                                  By = -Ax – C     ** divide every term by B**
                                                    Y = -A/B x + -C/B

Read

 

Go to your textbook to find out how to convert the equation of a linear function into general form. As you read, find out the answers to these questions:

• How do you know by what number you need to multiply both sides of the equation?
• How do you know which side of the equation in which to collect the terms?

Mathematics 10C Learn EveryWare © 2010 Alberta Education