Print this chapterPrint this chapter

Lesson 4: General Form and Slope-Point Form

Math 10C Module 5: Lesson 4

Module 5: Linear Functions

 

Did You Know?

 

A variation of general form that you will see in the next module is called standard form. The standard form of the equation of a line is Ax + By = C, where A, B, and C are integers and A and B cannot both be equal to zero.

Self-Check

 

SC 4. Convert the following equations into general form.

Compare your answers.

 

You can also convert an equation in general form to slope-intercept form. This is useful if you wish to identify the slope or y-intercept of a function prior to graphing it. Study the next example to see how this is done.

Example

A linear function is described by the equation 4x − 3y + 12 = 0. Identify the slope and y-intercept of the graph.

Solution

You can rearrange the equation into slope-intercept form in order to identify the slope and y-intercept.

 

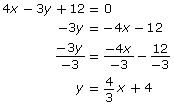
The slope is and the y-intercept is 4.

Once you have determined the slope and the y-intercept, you can then sketch an accurate graph of the linear function. In the next lesson you will learn strategies for graphing linear functions in general form. One strategy will be to rearrange the equation into slope-intercept form first.

You have now learned about three ways of expressing the equation of a linear function. In this next Self-Check problem, you have an opportunity to work with each one.

Self-Check

 

SC 5. The following graph shows the progress of a person who is walking his dog.

 

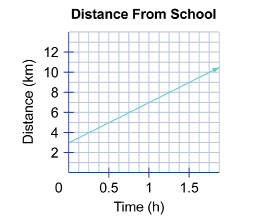
This shows the graph of distance from school versus time.

  1. State the coordinates of two convenient points on the line.
  2. Use the slope formula to determine the slope of the line.
  3. Write the equation of the line in slope-point form using one of your points from question a.
  4. Convert the equation into slope-intercept form.
  5. State the coordinates of the y-intercept, and explain what the y-intercept means.
  6. Convert the equation into general form.

Compare your answers.

 

You have studied slope-intercept, slope-point, and the general form of a linear function. Two linear functions are equivalent if they have the same slope and pass through the same point. Equivalent forms will have the same slope and y-intercept.

Try This 1 - 2

 

Print (or copy by hand) and complete the following in your course folder binder.

Try This 1 - 2 questions

Use the link below to check your answers to Try This 1 - 2.

Possible TT1-2 (Try This 1-2) Solutions.

 
Watch and Listen

Go to the following site to watch a video on converting forms.

-----------------------------------------------------------------------------

Go to the following site to look at a few more examples. Scroll to the bottom and do the short self test there.