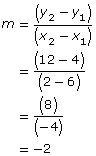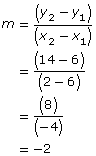Lesson 3: Parallel and Perpendicular Lines
Module 6: Linear Equations
Explore
© Wirrsing/18737250/Fotolia
Parallel and perpendicular lines can be used as a tool for constructing art. A mural is a work of art that is painted or drawn on a large surface, such as a wall or a ceiling. A mural can be found on the exterior wall of a building or on an interior wall in buildings such as schools, hospitals, or art galleries. Murals are often enlarged versions of smaller pictures or photos. To transfer an image to the wall, one approach is to overlay a grid onto the source image. A larger, but corresponding grid would be constructed on the wall. In this way, the artist can concentrate on painting the image “one grid square at a time.”
In the case of the preceding picture, the artist has divided the mural into 30 smaller sections. Which section do you think would take the longest time to paint? Which one would not take very much time to paint?
In this lesson you will examine how the slopes of both parallel and perpendicular lines are related. You will then apply this knowledge to the construction of linear equations.
Glossary Terms
Add these terms and their definitions to the Glossary Terms section in your notes You may also want to add examples that demonstrate how each term is applied.
- converse statement
- negative reciprocal
- parallel lines
- perpendicular lines
-----------------------------------------
Watch and Listen
Use the math is fun site Perpendicular and Parallel lines to get a further sense of parallel and perpendicular lines.
Pay close attention to the use of terminology, some of which might be new to you. Could any of these terms be used to improve your response to the analysis questions in the Math Lab?
You may have noticed in the Math Lab and in the site that the slopes of parallel lines are equal. This can be written as an if-then statement:
“If two lines are parallel, then their slopes are equal.”
Now consider the converse of this statement. The converse can be thought of as the reverse of this statement:
“If the slopes of two lines are equal, then they are parallel.”
Is this statement true? Find out by trying the next exercise.
Try This 1
Complete the following in your binder.
Try This 1 Questions
Use the link below to check your answers to Try This 1.
Possible TT1 Solutions
Example 1
Line EF passes through E(6, 4) and F(2, 12). Line CD passes through C(6, 6) and D(2, 14). Are the lines parallel? Justify your answer.
Solution
Determine the slopes of each line.
|
Line EF |
Line CD |
|
|
|
Since the slopes are the same, the lines are parallel.
Self-Check
You should have at least two sets of perpendicular lines from Part B of the Math Lab. Apply these questions to each set.
SC 1. Multiply the slopes of two perpendicular lines. What do you get?
SC 2. Describe the procedure you can follow to convert the slope of one line into the slope of another line that is perpendicular to the first one.
Try This 2
Once you have completed SC 1 and SC 2 and reviewed the answers, complete TT 2. If you need some assistance completing the question, read the following My Guide section.
TT 2. Prepare a demonstration of a way to test the validity of this statement:
If two lines are perpendicular to each other, then their slopes will have a product equal to –1.
Include the following:
- Write down the steps you followed so that your teacher or another student can duplicate your procedure, if necessary.
- Explain why the strategy was used, and describe how it supports the validity of the statement.
Remember that if you need some assistance, you can check the My Guide section in the lesson that shows one way that you can approach this task.
Possible TT2 Solutions
My Guide (click on materials list to get a drop down list)
Materials
-
grid paper
-
protractor
Step 1: Plot a point with integer coordinates. Choose a point that is near the centre of the grid, though not necessarily the origin itself. Call this point A.
Step 2: Apply a slope of 
to your point to find and mark a second point B.
Step 3: Join the two points A and B with a line that spans across the entire grid.
Step 4: Choose a point on the line with integer coordinates. This can be one of the two points that have already been plotted or another point on the line. Call this point C.
Step 5: Use the 
method to apply a slope of 
to point C. Locate the new point and call this point D.
Step 6: Join the points C and D with a line that spans across the entire grid.
Step 7: Use a protractor to measure the angle of the lines at their point of intersection. Are the two lines perpendicular?
Step 8: State your conclusions about the validity of the statement, “If the slopes of two lines are negative reciprocals, or have a product of −1, then the lines are perpendicular to each other.”
Work through the next example to see how you can find the slope of a line given specific information about a second line.
Example 2
Determine the slope of a line that is perpendicular to the line passing through G(4, 6) and H(2, 3).
Solution
Determine the slope of line GH.
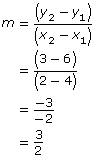
Then we can use
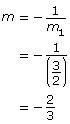
Therefore, the slope of the perpendicular line would be 
Tips
You already know that horizontal lines are perpendicular to vertical lines. Their slopes, however, are not readily identified as negative reciprocals. Therefore, you should keep in mind that a line with a slope of zero will always be perpendicular to a line with a slope that is undefined.