Lesson 4: Solving Linear Systems by Elimination

Module 7: Lesson 4

Module 7: Systems of Linear Equations

Explore

This shows a photo of various shoes scattered on the ground.

Study the photo with various shoes scattered on the ground. How many pairs of shoes can you find? Have you ever experienced the frustration of not being able to find a missing shoe or a missing sock?

There are many examples of occasions when you need to find a pair. In terms of clothing, you may need to find matching pairs of socks, mitts, shoes, earrings, or knee pads. You may also want to find a matching top and bottom to wear.

You need to find matching pairs in games such as Memory and Go Fish. After you’ve found a match, you can remove the cards from the playing area and they are no longer a part of the game.

In this lesson you will learn another algebraic method for solving a system of equations. The basis for this method is to match like terms and eliminate them by adding or subtracting the equations in the linear system. You may have to manipulate the equations before you can find the match.

Glossary Terms

Add these terms and their definitions to the Glossary Terms section in your notes. You may also want to add examples that demonstrate how each term is applied.

additive inverses
elimination method

------------------------------------------------------

In Math Lab: Properties of Linear Systems, you observed that the graph of a linear equation formed by adding or subtracting the equations of a linear system also passes through the point of intersection. You also noticed that by adding or subtracting equations, you may end up with a result where a variable has been “eliminated.”

You may still have questions about these observations and how they can be used to solve linear systems. In fact, the practice of adding, subtracting, and even multiplying equations is a practice that is fundamental to the algebraic method of solving a linear system by a method known as elimination. Try the next exercise to see how the elimination method works.

Try This 1 - 3

Complete the following in your course folder ( binder).
Try This 1 - 3 Questions
Use the link below to check your answers to Try This 1 - 3.
Possible TT1-3 Solutions

Self-Check

Solve the following linear systems by applying the elimination method.

SC 1.

x − 3y = 1
2x + 3y = 26

SC 2.

5x + 4y = 20
3x + 4y = 24

Compare your answers.

------------------------------------

In the linear systems that you have worked with, you have been able to eliminate a variable by adding or subtracting the given equations in the system. Sometimes it is not possible to eliminate a variable just by adding and subtracting. You may need to manipulate the equations in some way in preparation for elimination.

Try the next activity with a partner ( if possible) to see how you can do this. Recall from your results in Math Lab: Properties of Linear Systems that multiplying each term in a linear equation by a constant does not change the solution of the linear system. With this in mind, work with a partner to solve the systems of linear equations in the following activity.

Share 1 - 3

Print the questions out and complete them with another classmate or appropriate partner ( if possible).
Share 1 - 3 Questions

Use the link below to check your answers to Share 1 - 3.
Possible S1-3 Solutions

-----------------------------------

Work through the next example to see a couple of ways that you can solve a system of linear equations by elimination.

Example

Consider the following linear system:

6a − 5b = 14

4a + 3b = 22

Solve the linear system by using the method of elimination.
Verify the solution.

Solution

In this case, it is not possible to eliminate a variable by adding or subtracting the equations as they are. However, it is possible to eliminate either the a terms or the b-terms. Note: In the method of elimination, you are only looking for a way to eliminate one of the variables, not both!
Method 1: Eliminate the a-Term
To eliminate the a-term, you must multiply each equation by a constant so that the coefficients of the a-terms are either equal or additive inverses of each other. One way to determine this constant is to first determine the lowest common denominator of the current coefficients. Then multiply each equation by the factor that would result in a new coefficient equal to the lowest common multiple.
In this case, the lowest common multiple of 6 and 4 is 12. Since 2 × 6 = 12, and 3 × 4 = 12, the first equation should be multiplied by 2 and the second equation multiplied by 3.

2(6a − 5b) = 2(14)

3(4a + 3b) = 3(22)

12a − 10b = 28

12a + 9b = 66
To eliminate the a-terms, you must subtract the equations.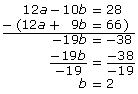

You can now determine the a-value by substituting b = 2 into one of the original equations.

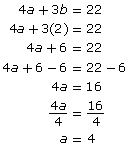
Method 2: Eliminate the b-Term
To eliminate the b-term, you must multiply each equation by a constant so that the coefficients of the b-terms are either equal or additive inverses of each other. You can find this constant by following the procedure in Method 1, where you first determine the lowest common multiple, or you could simply multiply each equation by the coefficient of the other equation.
In this case, you can multiply the first equation by 3 and the second equation by −5.

3(6a − 5b) = 3(14)

−5(4a + 3b) = −5(22)

18a − 15b = 42

−20a − 15b = −110
To eliminate the b-terms, you must subtract the equations.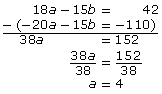

You can now determine the b-value by substituting b = 2 into one of the original equations.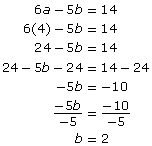
To verify the solution, substitute the a-value and b-value into the original equations.

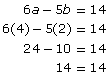
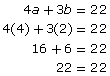
Since both equations are true, the solution is verified.

Share 4 - 7
Discuss the following questions with a partner ( if possible). Note down your answers in your course folder.

4. a. In both Method 1 and Method 2, substitution was avoided when determining one of the values. How can you avoid using substitution?

b. In what cases would it be better to not use substitution?

5. In both Method 1 and Method 2, the elimination method was based on subtracting the equations. How could you use addition to solve the system?

6. In what cases would you want to find the lowest common multiple of the two coefficients whose terms you are trying to eliminate?

7. In what steps in the solution do you think a student might commit an error?
Possible S4 - 7 Solutions