Lesson 5: Number of Solutions of a Linear System

Mathematics 10C Module 7 Lesson 5

Module 7: Systems of Linear Equations

Explore

This shows a photo of teenage actors rehearsing a play.

Comstock/Thinkstock

If you like to dance, sing, or act, you may want to consider participating in community theatre in your leisure time. Community theatre provides opportunities for people to work together to put on stage productions from one-act plays to full-scale musical productions. There are many community theatres all across Alberta from the small towns to the big cities. Some famous actors even got their start in community theatre!

The director of a community theatre production has many duties, one of which is to hold auditions. At auditions, people interested in getting a role in the production showcase their acting skills privately in front of the director. Based on the auditions, the director can make decisions about how to cast the play. For a particular role, the director may find one ideal candidate, no candidates, or many candidates. If there are many candidates for a role, then the director may decide to offer the role to two people and have each person alternate performances, especially in the case of a long production run where the show is staged multiple times.

In this lesson you will analyze the graphs and equations of linear systems to determine the nature of the solutions. Just as in the case of a director, you may find instances when there is a single solution, no solution, or infinitely many solutions!

In Lesson 1 you investigated solving systems of linear equations by graphing. In that lesson, you only encountered situations where each system had a unique solution. In other words, there was only one point of intersection. The coordinates of this point represented the values of x and y that satisfied both equations in the system. It is also possible for two lines to intersect infinitely many times or to never intersect.

Glossary Terms

Add these terms and their definitions to the Glossary Terms section in your notes. You may also want to add examples that demonstrate how each term is applied.

coincident lines
consistent system
dependent system
inconsistent system
independent system

---------------------------------------

Watch and Listen

Go to the Math Dude and watch a video about "Solving systems of equations".

Watch the video from the 3:30 mark to the end. (This is the same video from Lesson 1 that you started watching to he 3:30 point). Are the graphs that are presented in the video the same as the ones you generated in TT 4? As you watch, see if you can find a way to recognize the number of points of intersection by analyzing the equations in the system prior to graphing. You may want to press pause to momentarily stop the video when the equations are displayed.

--------------------------------------------

In the Discover section you considered the different ways that two straight lines can intersect. You may have come up with the following three possibilities.

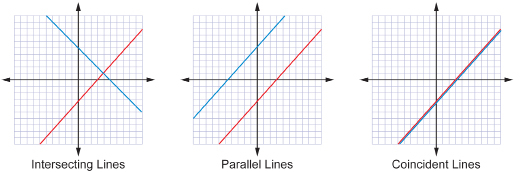
This shows an illustration of three graphs. The first graph shows two intersecting lines. The second graph shows two parallel lines. The third graph shows two coincident lines.

Try This 8

Complete the following. You will complete a table that is related to the three graphs you have just studied.
Try This 8 Questions
Use the link below to check your answers to Try This 8.
Possible TT8 Solutions

You can always determine the number of intersection points and solutions of a linear system by graphing the equations in the system. Sometimes, however, this may be inefficient or impractical.

In the remainder of this lesson, you will develop methods for identifying the number of solutions in a linear system by analyzing both the properties of the equations in the system.

Try This 9 - 12

Complete the following. You will again refer to the three graphs you have just studied. Work with a partner to complete TT 11 if possible.
Try This 9 - 12 Questions
Use the link below to check your answers to Try This 9 - 12.
Possible TT9 - 12 Solutions

Read

Go to your textbook to see how you can identify the number of solutions of a system by analyzing the slope and the y-intercepts of the linear equations. As you read, try to find out the answers to the following questions:

Why is it unnecessary to check the y-intercepts of the equations if the slopes are identified as unequal?
Why is it necessary to check the y-intercepts of the equations if the slopes are identified as equal?

Foundations and Pre-calculus Mathematics 10 (Pearson)

Read “Example 1: Determining the Number of Solutions of a Linear System” on pages 444 and 445.

Complete the following questions to check your understanding of the concepts covered in this lesson so far.

Self-Check

Determine the slopes and y-intercepts of each system; then identify the number of solutions for the system. In your response, be sure to include reasons that support your answer.

SC 1.

y = x + 1

y = x - 2

SC 2.

2x + 3y = 12

4x + 6y = 24

SC 3.

7x - 4y = 8

7x + 4y = 8

Compare your answers.

So far, you have studied two methods of determining the number of solutions of a linear system:

Method 1: You can graph the equations of the system and check the number of points of intersection.
Method 2: You can compare the slopes and the y-intercepts of each equation in a system.

In the next part of the lesson, you will investigate a third method based on an inspection of the equations in the system when written in standard form. Recall that standard form is when the equation of a line is written in the form Ax + By = C.

Share 1 - 2

Complete the following.
Share 1 - 2 Questions
Use the link below to check your answers to Share 1 - 2.
Possible S1-2 Solutions