Print this chapterPrint this chapter

Lesson 5: Number of Solutions of a Linear System

Mathematics 10C Module 7 Lesson 5

Module 7: Systems of Linear Equations

Connect

In this lesson you have discovered that a linear system can have a number of different solutions or no solutions at all. You created a flow chart that helps you to identify the number of solutions of a system based on its equations. As you undertake the tasks in this section, refer to your flow chart often to support your work.

Lesson Assessment

Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete. 

Project Connection **NOT ASSIGNED**

This shows a photo of a movie clapboard.

© Pedro Nogueira/

1893623/Fotolia

Depending on where you are vacationing, you may have opportunities to attend a live performance. You could attend a dramatic production, a live concert, a magic show, or a standup comedy performance. As part of your final module project, you will put your own abilities to the test by creating a performance piece about the concepts that you have learned in this module.

 

Go to the Unit 4 Project, and complete the Module 7: Lesson 5 component of the project.

 

 
Going Beyond

 

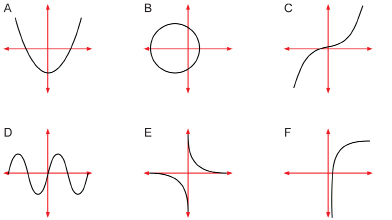
This shows an illustration of six non-linear graphs.

 

How can a system of equations contain exactly two solutions?

A system of linear equations cannot have exactly two solutions, since two lines cannot intersect exactly twice. However, in the case of non-linear systems, where at least one equation in the system is not represented by a straight line, then it is possible to have exactly two solutions.

Part A

The illustration above shows some non-linear graphs that you may encounter in future math courses.

  1. For each of the graphs shown in the illustration, state all possible solutions for a system of equations comprised of a linear equation and an equation represented by the graph. In other words, determine how many different ways a straight line can intersect each of the graphs above.

    You may want to print out a copy of these graphs and then use a ruler, pencil, or other straightedge to see how many ways a straight line can intersect each graph. For example, a straight line can intersect Graph A once, twice, or not at all. Therefore, the system could have one solution, two solutions, or no solutions.

Part B

How would you solve a non-linear system algebraically?

  1. See if you can use a method that you have learned in this module to solve the following non-linear systems.

    1. y = -3
      y = x2 - 3

    2. x - y = 2
      (x + 2)2 + y2 = 16

Save your responses in your course folder. Your teacher may choose to examine your work at a later time.

Â