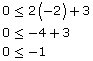Lesson 6: Solving Problems with Linear Systems

Module 7: Lesson 6

Module 7: Systems of Linear Equations

Connect

Lesson Assessment

Complete the lesson quiz posted under the Quizzes link to the left in moodle or under the Assess tab and ensure your work in your binder (course folder) is complete.

Project Connection NOT ASSIGNED

This shows an illustration of silhouettes against a green, starry background. The silhouettes depict four jumping teens, some palm trees, and a jet airplane flying in the sky.

iStockphoto/Thinkstock

You will now have an opportunity to return to the other Project Connections in this module to complete what you have previously started.

Go to the Unit 4 Project, and complete the Module 7: Lesson 6 component.

Going Beyond

Throughout this module, you have modelled and solved systems of linear equations. Some problems can be modelled by solving a system of linear inequalities.

Part A

Step 1: Use graph paper or the Graph Paper Template to graph the equation y = 2x + 3. The line that you graphed divides the coordinate plane into two half-planes.

Step 2: Go to the Pairs Table document. Choose any three points on one side of the line and record them as ordered pairs in the left-hand column in the table provided in the document. Make sure to save your Pairs Table document to your course folder.

Step 3: In the right-hand column of the table in the Pairs Table document, substitute the coordinates of each ordered pair into the expression. Simplify the expression and decide if the final expression is true or false. An example is shown below.

(x, y)

(-2, 0)

eqn103.eps

False, since 0 is greater than -1.

Step 4: Repeat steps 2 and 3 for three points on the other side of the line, in the other half-plane. Remember to save your updated Pairs Table document to your course folder.

Step 5: You may have noticed that one half-plane contains points that yield true expressions, whereas the points in the other half-plane leads to false expressions. Shade in the half-plane that yields true expressions. This is the graph of the linear inequality since all of the points in the shaded region represent ordered pairs that satisfy the inequality.

Step 6: Follow a similar procedure to graph a second inequality on the same set of axes as the previous one. Start by graphing x + 2y = 4; then apply steps 2 to 4.

Part B

With a partner, discuss the following questions and come up with some responses. You may search the Internet for related topics to supplement your discussion. Record your responses and save them in your course folder.

a. Where do the graphs of the linear inequalities intersect?
b. How is this different from the intersection of two linear equations?
How many solutions are there for this system of linear inequalities?
What real-life situation could be modelled by a linear inequality or a system of linear inequalities?
Sketch a system of linear inequalities that has no solution. You do not need to write the system itself.

Save your responses in your course folder.