Print this chapterPrint this chapter

Lesson 1

1. Lesson 1

1.3. Refresher

Mathematics 20-2 M1 Lesson 1

Module 1: Trigonometry

 
Refresher
 

This section will help refresh your memory on the use of primary trigonometric ratios and the Pythagorean theorem. Look at this section if you had difficulty with the questions from Are You Ready?

 

You may find it helpful to review Three Sides of a Right Triangle from the Mathematics 10C course.

 

 

This play button opens up Three Sides of a Right Triangle.

 

The definitions for the primary trigonometric ratios are given in the following table.

 

Trigonometric Ratio Definition Formula
sine the ratio of the length of the side opposite the reference angle to the length of the hypotenuse
cosine the ratio of the length of the side adjacent to the reference angle to the length of the hypotenuse
tangent the ratio of the length of the side opposite the reference angle to the length of the side adjacent to the reference angle


The interactive piece titled “Exploring Trigonometry” allows you to practise identifying the sides of a triangle by dragging and dropping the opposite, adjacent, and hypotenuse sides into their correct locations. You can find the interactive piece on the right-hand side of the website.

 

 

This is a screenshot for Exploring Trigonometry.

 

The sine, cosine, and tangent ratios can be used to determine lengths of sides and measures of angles. When you open the piece titled Finding Angles and Lengths Using Sine, Cosine, and Tangent Ratios, you can view examples of how each ratio is used.

 

 

This is a screenshot for Finding Angles and Lengths Using Sine, Cosine, and Tangent Ratios.

 

Under the Finding Angles box, click “Sine,” “Cosine,” and “Tangent” to see examples of how each ratio can be used to determine missing angles depending on the information that you have. Then, under the Finding Lengths box, click “Sine,” “Cosine,” and “Tangent” to see examples of how each ratio can help to find missing side lengths in a right triangle.

You should now be more comfortable using the primary trigonometric ratios.

 

The Pythagorean theorem is defined as a2 + b2 = c2 where a and b are sides adjacent to the right angle and c is the longest side, called the hypotenuse.

 

Example 1

 

Find y. The answer should be rounded to the nearest tenth of a metre.

 

 

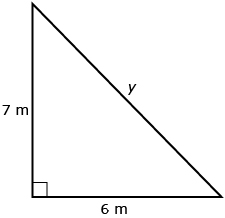
This is a picture of a right triangle. The hypotenuse is labelled y, and the other two sides are 6 m and 7 m.

 

Use the Pythagorean theorem.

 

 

 

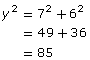
Take the square root of both sides.

 

 

y = 9.2 m

 

Example 2

 

Determine x.

 

 

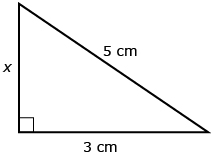
This is a picture of a right triangle. The hypotenuse is 5 cm, one side is 3 cm, and the last side is labelled x.

 

Use the Pythagorean theorem.

 

 

 

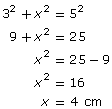
Go back to the section titled Are You Ready? Try the questions again. If you are still having difficulty, contact your teacher.