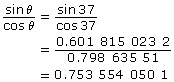Lesson 2

In the previous activity you saw that the Pythagorean theorem is only valid for right triangles. What about the primary trigonometric ratios—can they be used to solve for missing measurements in oblique triangles? A close examination of these ratios will answer this question.

• 
  
  
• 
  
  
• 

The sine and cosine ratios require the length of the hypotenuse. Since the hypotenuse is defined to be the side across from a right angle, you can only talk about hypotenuse if you have a right triangle. For this reason, the sine and cosine ratios only make sense for a right triangle.

 

Another way to define the tangent ratio is using the sine and cosine ratios.

 

 

You can check this using any acute angle. Try 37° and put each side of the equation into a table.

 

 

Since the tangent ratio can be written as the quotient of the sine and cosine ratios, the tangent ratio will also only work for right triangles.