Lesson 2

1. Lesson 2

1.7. Explore 4

Mathematics 20-2 M1 Lesson 2

Module 1: Trigonometry

The sine law can also be used to solve for angles. When using the sine law, rearranging the formula is easier when the unknown is in the numerator. The following equivalent form of the sine law is usually used when solving for angles:

Read “Communication Tip” in the margin of page 136 of your textbook to learn about compass directions.

This is a photo of a compass sitting on a map.

BananaStock/Thinkstock

Example

Jeremy is learning how to use a compass in an orienteering course. The instructions he was given tell him that he must walk 70 m from Checkpoint A to Checkpoint B. He knows that Checkpoint A is directly north of him and Checkpoint B is in a direction of N41°E. He also knows that Checkpoint B is 105 m from Checkpoint C. He begins by drawing a diagram to represent his situation.

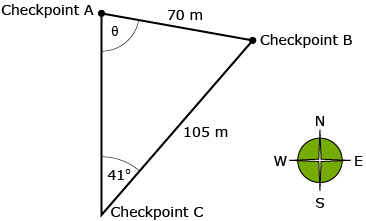
This picture shows an oblique triangle with vertices labelled Checkpoint A, Checkpoint B, and Checkpoint C. The angle at Checkpoint C is 41 degrees, the angle at Checkpoint A is labelled theta, the side across from angle theta is 105 m, and the side across from the 41 degree angle is 70 m.

Jeremy needs to determine the direction to walk when going from Checkpoint A to Checkpoint B.

From the diagram he drew, he knows that once he determines angle θ he will be able to state the direction as Sθ°E. Jeremy looks at the given information and recognizes that he can use the sine law to determine this angle. His solution can be seen in the animation Jeremy’s Solution: Example 2.

Read “Example 3: Using reasoning to determine the measure of an angle” on page 136 of your textbook. As with the preceding example, Anthony has been asked to determine a direction. You will learn more about parallel lines and transversals, which are used in the second half of Anthony’s solution in Module 2: Logic and Geometry.

Ensure that you are comfortable with the steps in this solution before moving on.