Lesson 3

Explore

 

What Jennifer and David did in their solution was to derive an equation called the cosine law. It’s a “law” because none of the steps relied on specific measurements for sides or angles. As a result, those steps and the final result are valid for any acute triangle. (The cosine law is actually valid for any triangle, including obtuse triangles, but a slightly different derivation is required.)

 

The cosine law is usually written in the following way:

 

a2 = b2 + c2 − 2bc cos A

 

Recall from Lesson 2 that mathematicians typically label sides with lowercase letters and angles with uppercase letters. Furthermore, sides and angles with the same letter are across from each other. For instance, side a is across from ∠A.

 

 

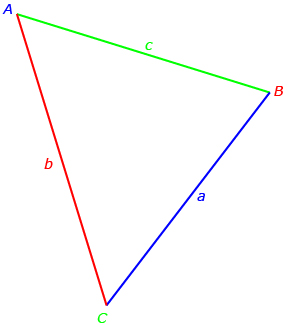
Keep this naming convention in mind. A in the equation must be the measure of the angle across from side a, which is the one you’ll be trying to determine. Look closely at the equation (a2 = b2 + c2 − 2bc cos A). In order to determine the length of one side—a in the equation—you must know the following:

• the lengths of the other two sides (b and c)
• the angle across from the side you’re trying to determine (A)

You can use the Cosine Law Explorer applet to see that the cosine law is valid for any triangle. Drag the vertices of the triangle and confirm that the left side of the cosine law is always equal to the right side.

 

 

The animation titled Cosine Law Illustrator may help you better understand the relationships among a, b, c, and ∠A in the cosine law.