Print this chapterPrint this chapter

Lesson 4

1. Lesson 4

1.4. Explore

Mathematics 20-2 M1 Lesson 4

Module 1: Trigonometry

 
Explore
 

In this lesson you will use your experience to determine whether to use the sine law or the cosine law to solve problems that require more than one triangle. Problems may include right triangles, oblique triangles, or both.

 

The first problem in the Focus section will now be revisited.

 

Example 1

 

Joey is flying a kite and wants to determine its height. He enlists the help of his friend, Jahnavi, who is standing 90 m away. Joey uses a clinometer and determines that the angle of elevation to the kite is 62°. Jahnavi determines that the angle of elevation is 37°. To keep calculations simple for this question, ignore Joey’s height and assume that the kite string touches the ground.

 

Jahnavi starts by drawing the following diagram.

 

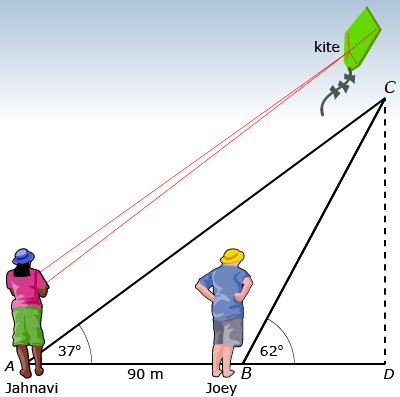
This picture shows Jahnavi, Joey, the kite, and two angles of elevation. There is a large right triangle with vertices A, D, and C. Side AD is parallel to the ground, side DC is perpendicular to the ground, and side AC is the hypotenuse. Angle A is 37 degrees, and angle D is 90 degrees. A second right triangle with vertices B, C, and D is contained within the first right triangle. Point B is on segment AD. Angle B is 62 degrees. Jahnavi is at point A, Joey is at point B, and segment AB is 90 m.

 

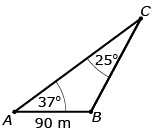
After drawing the picture, Jahnavi realized there are three triangles in this diagram: , , and . Since and share side BC, she decided to use a three-step approach:

 

Step 1: She will use her knowledge of straight angles and sums of angles in triangles to determine ∠ABC and ∠ACB.

 

Step 2: Use to determine the length of BC.

 

Step 3: Use to determine the height (CD).

 

Step 1 of Jahnavi’s Solution

 

 

∠ABC + 62° = 180°

 

∠ABC = 118°

Straight angles add to 180°.

37° + 118° + ∠ACB = 180°

 

∠ACB = 25°

The sum of the angles in any triangle is 180°.

 

Step 2 of Jahnavi’s Solution

 

 

This picture shows an oblique triangle with vertices A, B, and C. Angle A is 37 degrees, angle C is 25 degrees, and side AB is 90 m.

 

is not a right triangle, thus the primary trigonometric ratios cannot be used. Jahnavi has chosen to use the sine law.

Jahnavi multiplied both sides of the equation by sin 37° in order to isolate BC.

BC = 128.1614…

Jahnavi has not rounded this number because it is not the final answer.

 

 

Step 3 of Jahnavi’s Solution

 

 

This is a picture of a right triangle with vertices B, C, and D. Angle B is 62 degrees, and angle D is 90 degrees.

 

is a right triangle, thus Jahnavi can use SOH CAH TOA.

CD = (128.1614… sin 62°

Multiply both sides of the previous equation by 128.1614…

CD = 113.1598 m

The unrounded value of CD is 113.1598 m.

CD = 113.2 m

The kite is 113.2 m above the ground.