Lesson 4
1. Lesson 4
1.5. Explore 2
Module 1: Trigonometry
Example 2
Jeremy is on the third day of his orienteering course and has been asked to determine the distance from point A to point D. He knows some distances and angles as shown in the following diagram.
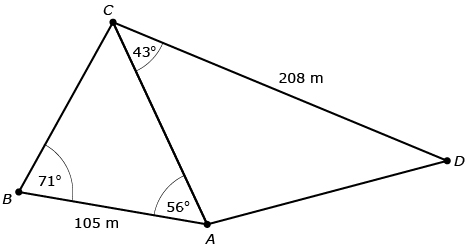
Jeremy noted that 
and 
share side AC. As a result, he can use 
to solve for side AC; and then he can use 
to solve for length AD.
|
Step 1 of Jeremy’s Solution |
|
|
∠BCA = 53° |
Jeremy knows that the sum of the angles in a triangle is 180° and uses that to calculate the measure of ∠BCA. |
|
|
|
|
|
Jeremy multiplied both sides of the equation by sin 71° in order to isolate AC. |
|
AC = 124.3113… |
The unrounded value of AC is 124.3113… |
is not a right triangle. Jeremy chooses to use the sine law to calculate AC.
|
Step 2 of Jeremy’s Solution |
|
|
AD2 = AC2 + 2082 − 2(AC)(208) cos 43° |
Jeremy applies the cosine law to |
|
AD2 = (124.3113…)2 + 2082 − 2(124.3113…)(208) cos 43° |
Jeremy uses the unrounded value for AC by pressing the ANS key on his calculator. |
|
AD2 = 20 896.4368… |
The unrounded value of AD2 is 20 896.4368… |
|
|
Take the square root of both sides to solve for AD. |
|
AD = 144.5559… |
The unrounded value of AD is 144.5559… |
|
AD = 144.6 m |
The distance from point A to D is 144.6 m. |
using AC calculated in step 1. 
Did You Know?
Canada’s First Nations people were the first map makers in Canada. Undoubtedly, their maps were useful to the European explorers of the 1400s. However, these maps had two significant differences to what the Europeans would have been used to using:
- First Nations’ maps were usually memorized and only drawn when required to communicate locations and distances with others.
- The scale of the maps often corresponded to travel time rather than absolute distances. As a result, two identical real-world distances would not be identical on the map if one required more travel time due to rough terrain.
Read “Example 3: Solving a three-dimensional problem” on page 159 of your textbook. Notice how Diana breaks the problem’s solution into two steps—in the first step, she uses the sine law to determine the length of side BC. In the second step, she uses the tangent ratio to determine the height of the cliff.
Ensure that you are comfortable with the steps in this solution before moving on.