Print this chapterPrint this chapter

Lesson 2

1. Lesson 2

1.4. Explore 4

Module 2: Lesson 2

Module 2: Logic and Geometry

 

This is a photo of a circular purple pillow.

PhotoObjects.net/Thinkstock

Try This 1
 

Vicky is working on a design for a quilted circular pillow. In her design, she is marking points on the circumference of the circle and then joining the points with line segments hint or chords hint to create regions. She is trying to determine how many different types of fabric she will need to cover the pillow top if each region is to be a different colour or pattern of fabric.

 

As she is drawing her sketch of the circular pillow design, she notices the pattern shown in the following sketch.

 

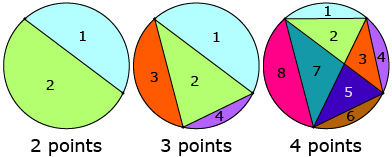
This is a graphic of three circles. The first circle is divided into two regions. The second circle is divided into four regions. The third circle is divided into eight regions.

  1. Based on Vicky’s sketch, make a conjecture about the relationship between the numbers of regions created within the circle and the number of points on the circumference of the circle.

  2. Use the Circle Conjecture applet to test the validity of your conjecture. As you test the conjecture, consider the following questions:

    • How many supported examples are needed for you to consider your conjecture to be valid?

    • Can you find a counterexample to disprove the conjecture?

       
      This is an applet that allows students to create regions in a circle by connecting points on the circumference of a circle. This graphic shows a conjecture that reads, “As the number of connected points on the circumference of a circle increases by 1, the number of regions created within the cirlces increases by a factor of 2.”
Share 3

 

Share your findings from Try This 1 with another student or appropriate partner either in person or virtually. Use the following questions to guide your discussion.

  • Explain the conjecture you developed for the relationship between the number of regions created within the circle and the number of points on the circumference of the circle.

  • Present your opinion on the amount of examples or evidence required to test the conjecture. How does it compare with your partner's opinion?

  • Identify a counterexample, if applicable. What does this tell you about your conjecture?
a line segment with endpoints on a curve
a part of a line between two endpoints along the line