Lesson 3
1. Lesson 3
1.4. Discover
Module 2: Logic and Geometry
Discover
Arithmagons are number puzzles whose central operation is addition. Arithmagons are based on polygons. For example, a triangular arithmagon has 3 sides while a pentagonal arithmagon has 5 sides. There is a circle at each vertex and a box on each side of an arithmagon.
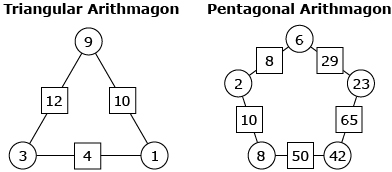
Try This 1
The following Arithmagons applet contains various triangular arithmagons to solve. This activity requires that you apply what you have learned about reasoning to solve arithmagon puzzles.
Follow the instructions in the applet for completing the arithmagons activity.
As you discover the solution to the arithmagons using your own personal strategy, think about any patterns that might be present. For instance, consider what relationship exists (if any) between the
- numbers in the circles and the numbers in the boxes
- number in a circle and the number in the box opposite a circle
Record your conjectures about possible patterns in the arithmagons in your course folder. Once you have completed the applet, you will be sharing your conjectures and thoughts with others in the Share 1 activity. It is important that you keep your responses in a location where they are readily accessible.
Share 1

Marili Forastieri/Digital Vision/Thinkstock
Work with a partner or in a group to discuss your findings from Try This 1.
- Present your conjecture about any patterns you identified about arithmagons in Try This 1 to your group. Describe the pattern you think exists, and give an example of the pattern in an arithmagon. You may choose to present the pattern using words, pictorially, or another method of your choice.
- Once all members of your group have presented their conjectures, compare the patterns. In your discussions, consider the following:
- How are the patterns similar? (Are there any common elements between the patterns?)
- How are the patterns different?
- Do you agree with the patterns presented by other students? (Do the patterns work? Is there a counterexample that disproves the conjecture?) If you don’t agree with other patterns, identify why you think the pattern doesn’t work. (Can you find a counterexample? Can the conjecture be revised to work?)
- How are the patterns similar? (Are there any common elements between the patterns?)
- Based on the patterns you have been presented with, determine a method, strategy, or rule as a group that can be used to describe all arithmagons. The rule may be written out in words, explained using a graphic or algebra, or described using another method of your choosing. For instance, if you are using algebra to describe your solution or pattern, you would have to explain what values are in circles (a, b, and c) and what values are in boxes (d, e, and f) and how they are related.
