Print this chapterPrint this chapter

Lesson 3

1. Lesson 3

1.5. Explore

Module 2: Lesson 3

Module 2: Logic and Geometry

 

Explore
 

As you completed Try This 1 and Share 1 activities, you may have noticed a few different patterns in the arithmagons. You and your group might have made the following conjectures based on your observations of the patterns in the triangular arithmagons:

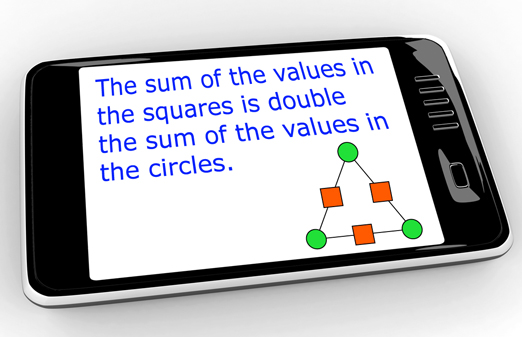
  • The number in each box is the sum of the two adjacent circle numbers.

     
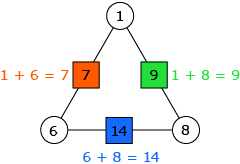
    This is a graphic of an arithmagon showing that the number in each box is the sum of the two numbers in the circles that are beside each box.
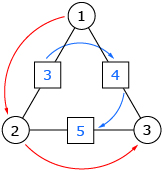
  • When the box numbers form a clockwise sequence, the circle numbers form a counter-clockwise sequence.

     
    This is a graphic of an arithmagon with the numbers 1, 2, and 3 in the circles and 3, 4, and 5 in the boxes.
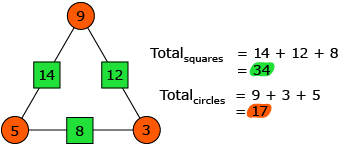
  • The sum of the values in the squares is double the sum of the values in the circles.

     
    This is a graphic of an arithmagon with the numbers 9, 5, and 3 in the circles and 14, 8, and 12 in the boxes.
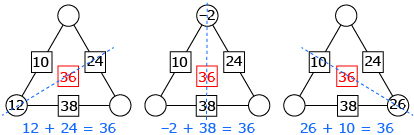
  • The sum of the value in a circle and the opposite box is the same number (i.e., the centre number).

     
    This is a graphic of an arithmagon showing the relationship between circles and their opposite squares, as well as the relationship between outer numbers and the centre number.

The conjectures you made in Discover were based on your observations of patterns in the triangular arithmagons. Inductive reasoning was used to arrive at your conjectures. Recall that conjectures cannot be proven using inductive reasoning. You cannot look at every possible arithmagon, so it is not possible to prove a conjecture using inductive reasoning. When you worked on Share, you and your group may even have revised some of the conjectures if a counterexample was found.

 

generalization: a statement, principle, or idea that has a general application

The aim of the activity you completed in the Arithmagons applet was to make conjectures about the solutions to triangular arithmagons based on observed patterns and to develop a rule that you can use to solve other triangular arithmagons. In other words, can a rule be written, based on the pattern(s) you identified, and successfully applied to all triangular arithmagons? This rule is known as a generalization.

This is a graphic of a handheld device with the conjecture “The sum of the values in the squares is double the sum of the values in the circles” written on the screen.

iStockphoto/Thinkstock

 

Consider the conjecture Wahid made about triangular arithmagons.

 

Wahid based his conjecture on evidence he gathered from arithmagons in the Arithmagon applet as well as several other examples.

 

proof: a logical or mathematical argument that shows a statement is valid in all cases, or that no counterexample exists1

Wahid and his friends Cynthia and Kyle decided they wanted to prove that Wahid’s conjecture was true for all triangular arithmagons. Watch the animation From Conjecture to Generalization to see how Wahid’s group developed its proof.

 

 

This is a screenshot for From Conjecture to Generalization.

 

Wahid and his friends proved that the sum of the values in the squares will always be equal to twice the sum of the values in the circles in all triangular arithmagons. The steps that Wahid, Cynthia, and Kyle used to determine that the generalization is valid in all cases are called a proof.

deductive reasoning: a type of reasoning used to draw a specific conclusion through logical reasoning by starting with statements that are accepted as true (valid)2

The process of generalizing a conjecture is called deductive reasoning. Deductive reasoning uses a well-developed system of logic to prove a conjecture. This kind of reasoning starts with general statements that are assumed to be true and derives specific conclusions. So deductive reasoning goes from the general to the specific. This is the opposite of inductive reasoning, which goes from the specific to the general. Inductive reasoning starts with specific assumptions and concludes something general.

 

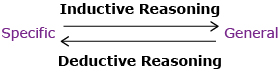
This is a graphic showing an arrow going from specific to general. The words “inductive reasoning” are placed above the arrow. Another arrow going from general to specific has the words “deductive reasoning” placed below it.

 

Recall that inductive reasoning can never be used to prove a conjecture. Since it is not possible to observe every known case, reasoning by induction is not logically valid. Inductive reasoning can be involved in the discovery process that produces conjectures, but deductive reasoning is required to prove the conjecture.

 

1, 2 Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 27. Reproduced by permission.