Lesson 3
1. Lesson 3
1.7. Explore 3
Module 2: Logic and Geometry
Self-Check 2
- Complete “Practising” question 17 on page 24 of your textbook. Answer
- Complete “Practising” question 9 on page 32 of your textbook. Answer
- Complete “Practising” questions 4 and 5 on page 31 of your textbook. Answer
Remember that the purpose of a proof is to show that the conjecture is true in all cases. The specific strategy that is used for a proof will vary based on the conjecture and the individual’s personal strategy for creating the proof. When deductive reasoning is used correctly in a proof, you can be sure that the conclusion you draw is valid.
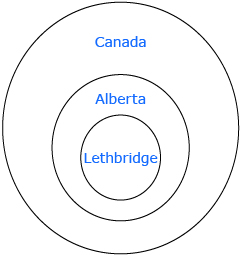
Not all proofs involve or require algebra. Proving a statement using deductive reasoning can be done in a variety of ways. Proofs might involve the organization and visualization of given statements in a Venn diagram to make a valid conclusion. For example, a Venn diagram can be used to prove that all people in Lethbridge live in Canada.
A two-column proof might also be used to prove a conjecture. You will look at more examples of two-column proofs later in this module when you look at possible strategies for proving geometric conjectures.
Venn diagram: a type of diagram used to picture sets and the relationships between them
two-column proof: a presentation of a logical flow of statements in the left-hand column and the reasons or justifications why each of these statements are valid in the right-hand column of a table
— Adapted from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11,
© 2012 Nelson Education Limited. p. 29. Reproduced by permission.
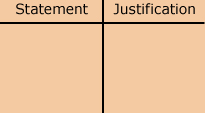
To see an example of a proof using a Venn diagram and an example with a two-column proof, read “Example 3: Using deductive reasoning to make a valid conclusion” and “Example 4: Using deductive reasoning to prove a geometric conjecture” on page 29 of your textbook. As you read the examples, consider how Venn diagrams and two-column proofs help to visualize and organize the statements.
If you haven’t done so already, now would be a good time to update your Glossary Terms document. Remember to save your updated document to your course folder.
Self-Check 3
- Complete “Check Your Understanding” question 2 on page 31 of your textbook. Answer
- Complete “Practising” question 8 on page 32 of your textbook. Answer
In this lesson you learned about the type of reasoning required to prove conjectures. If you haven’t done so already, update your notes organizer with any thoughts or key ideas about inductive and deductive reasoning. For instance, you might find it helpful to add an example of a proof. The “Mid-Chapter Review” on page 34 of your textbook provides some frequently asked questions you can use to get started.