Lesson 6

Try This 1

 

Use the applet Opposite Angles to determine the relationship between the angles formed by two intersecting lines. From your observations, what conjecture can you make about opposite angles? Move the position of the intersecting lines by clicking on the blue points on any of the lines. Does your conjecture still hold when you reposition the lines?

 

 

In Try This 1, you made a conjecture about opposite angles based on your observations. In Try This 2 you will expand on this by considering what relationships exist between angles when another line is added.

---

Try This 2

 

Use the animation Angles and Lines to investigate what relationships exist between the eight angles that are formed when two or more lines intersect. As you compare the measures of the angles, see what happens to the angles when you move various lines. For instance:

• What happens to the measure of the angles when you move line QR?
• What happens to the measure of the angles when you move line ST?
• What happens to the measure of the angles when you move line UV?
• Does it matter whether the lines are parallel or non-parallel?

---

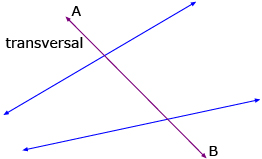
Try This 2 activity allowed you to examine angles formed when a line intersects two parallel or two non-parallel lines. When any two lines are intersected by a third straight line, we call that line a transversal. When a transversal intersects a pair of lines, two sets of angles are created.

 

 

 

 

 

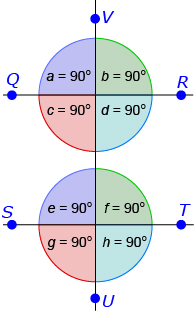
When the parallel lines QR and ST are intersected by the transversal UV, a total of eight angles are formed. UV intersecting QR creates angles a, b, c, and d. UV intersecting ST creates angles e, g, f, and h.

 

In Try This 3, you will focus on parallel lines intersected by a transversal. You will consider the relationships between all eight angles formed by this intersection.