Lesson 6

Lesson 6 Summary

 

The game fox and geese requires the movement of pieces along horizontal, vertical, and diagonal lines on a game board. The design of this game board is an important factor in how the game is played. The characteristics of the game were used in this lesson to investigate relationships between pairs of angles formed between intersecting lines. Based on evidence gathered in various applets, you developed conjectures about these angles and intersecting lines.

 

Some of the conjectures examined in this lesson can be summarized as follows.

 

When a transversal intersects two parallel lines, the following are true:

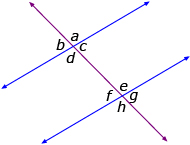
• The corresponding angles are equal (a = e, b = f, c = g, d = h). You can draw the letter F on the diagram to find corresponding angles.
  
  
   
  
  
  
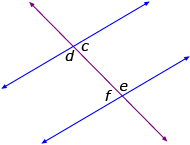
• The alternate interior angles are equal (c = f, d = e). You can draw the letter Z on the diagram; these angles are inside of the Z.
  
  
   
  
  
  
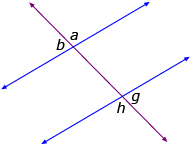
• The alternate exterior angles are equal (a = h, b = g). You can draw the letter Z on the diagram, and these angles are outside of the Z.
  
  
   
  
  
  
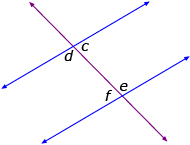
• The interior angles on the same side of the transversal (or consecutive interior angles) are supplementary (c + e = 180°, d + f = 180°). Draw the letter C on the diagram.
  
  
   
  
  

The converse of these conjectures was also supported by the evidence. In other words, if the angles are equal, the lines are parallel. The converse of the conjectures that were just presented is stated in the following way: When a transversal intersects two lines and creates

• corresponding angles that are equal, the two lines are parallel
  
  
• alternate interior angles that are equal, the two lines are parallel
  
  
• alternate exterior angles that are equal, the two lines are parallel
  
  
• interior angles on the same side of the transversal that are supplementary, the two lines are parallel

The evidence also showed that these relationships are only true for parallel lines and their transversals. These conjectures are not true for transversals that intersect two non-parallel lines.

 

Inductive reasoning was used in this lesson to develop the conjectures that are only true for parallel lines and their transversals. In Lesson 7 you will use deductive reasoning to attempt to prove these conjectures. Any proven conjectures would be known as angle-relationship properties. You will then use these properties to solve problems.