Lesson 9

Discover

Joe is teasing his brain with the Acute Dissection problem. He dissects the obtuse triangle into four smaller triangles as shown in the diagram. Then he uses a protractor to measure all of the angles. Joe concludes that since the four triangles in his diagram all have sums of 180°, then all triangles have sums of 180°. The following is what Joe considers his proof.

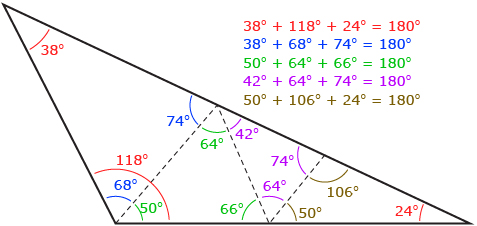
Is Joe’s evidence enough to prove that the sum of the interior angles in a triangle is 180°?

Joe used inductive reasoning in his solution. From previous lessons, you know that inductive reasoning cannot be used to prove a conjecture. The evidence Joe gathered strengthens the conjecture that the sum of the angles in a triangle is 180°, but it does not prove the conjecture.

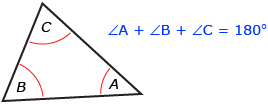
The sum of the interior angles of a triangle theorem may be one of the most well-known mathematical theorems. In previous courses you have been told that the sum of all three interior angles in a triangle is 180°, but you may never have proven that this is true for all cases.

In fact, in previous courses, you might even have folded the corners of a triangle together to show that all three interior angles of a triangle form a line.

Use the Interactive Triangle applet or the Folded Paper Triangle applet to investigate the sum of the interior angles of a triangle. In each applet, you can drag a vertex of the triangle to make triangles of varying sizes. As you change the triangles, does the sum of the angles in the triangles change?

The Interactive Triangle applet and the Folded Paper Triangle applet both illustrate that the sum of the interior angles of a triangle is 180°. But why is this? What is the reasoning behind this theorem? In the following Try This activity, you will prove that the measures of the three angles in any triangle—acute, right, and obtuse—have a sum of 180°.

Try This 1