Lesson 9
1. Lesson 9
1.2. Explore
Module 2: Logic and Geometry
Explore
In Discover you used the properties of angles formed by a transversal intersecting two parallel lines to prove the sum of the measures of the interior angles in a triangle is 180°. Watch the animation Proving the Sum of Interior Angles to see a proof developed by one student, Zahia.
If the proof you created in Try This 1 was invalid, go back to your original drawing. Make sure your lines are parallel. Remember that the properties of angles are only true when a transversal intersects two parallel lines, not two non-parallel lines.
As you have seen in previous lessons, deductive proofs can be created in many forms. The proof shown in the animation Proving the Sum of Interior Angles of a Triangle was presented as a series of statements that explained the student’s reasoning process. The reasoning could have also been presented in a two-column proof.
Given: ![]()
Prove: ∠DRE + ∠RDE + ∠RED = 180°
Proof:
|
Statements |
Justifications |
|
1. Draw |
A line can be drawn parallel to a given line through an external point not on the line. |
|
2. ∠PDQ = 180° |
A straight line angle measures 180°. |
|
3. ∠PDR + ∠RDE + ∠QDE = 180° |
The three angles form a straight line, so their sum is 180°. |
|
4. ∠DRE = ∠PDR and ∠RED = ∠QDE |
Alternate interior angles. |
|
5. ∠DRE + ∠RDE + ∠RED = 180° |
Substitution (a quantity may be substituted for an equal quantity). |
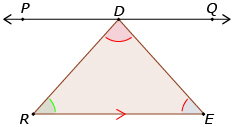
Therefore, the sum of the interior angles in a triangle is always 180°.
Regardless of the method, diagrams are useful to include in proofs as they provide a visual of the situation.
