Lesson 10

Explore

 

When designing structures that contain congruent triangles, there is a minimum set of angle and side measurements that can be given to ensure that the triangles constructed are the same. Remember that two or more triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in measure.

 

In Discover you showed that a minimum of three sets of measurements is required in order to establish congruency:

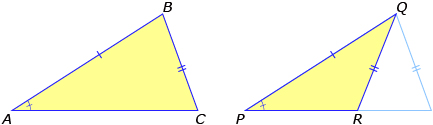
• SSS (side-side-side): If three pairs of corresponding sides are equal in length, then the triangles are congruent.
  
  
   
  AC = DF
  
   
  BC = EF
  
   
  AB = DE
  
  
   
  
  
  
   
  

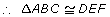
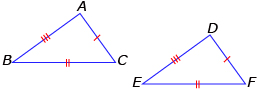
• SAS (side-angle-side): If two pairs of corresponding sides are equal in length, and the included angles are equal in measure, then the triangles are congruent.
  
  
   
  AB = DF
  
   
  ∠B = ∠E
  
   
  BC = EF
  
  
   
  
  
  
   
  

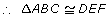
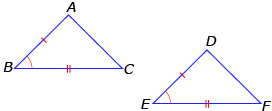
• ASA (angle-side-angle): If two pairs of corresponding angles are equal in measure and the included sides are equal in length, then the triangles are congruent.
  
  
   
  ∠B = ∠E
  
   
  BC = EF
  
   
  ∠C = ∠F
  
  
   
  
  
  
   
  

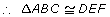
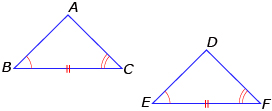
• AAS (angle-angle-side): If two pairs of corresponding angles are equal in measure and a pair of opposite sides is equal in length, then the triangles are congruent.
  
  
   
  ∠B = ∠F
  
   
  ∠C = ∠F
  
   
  AB = DE
  
  
   
  
  
  
   
  

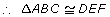
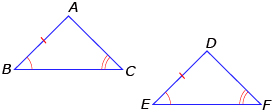
Not all mathematicians agree that AAS is a condition of congruency. Some believe that this is a special application of ASA. They support this statement as follows:

 

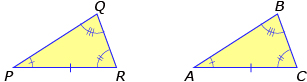
In order to have angle-angle-side (AAS) congruent, the third angle must also be congruent. By changing which angles to compare, ASA congruency is proved. Consider and . Since ∠Q = ∠B, ∠P = ∠A, and PR = AC, then ∠R = ∠C. ASA congruency would mean that ∠P = ∠A, PR = AC, ∠R = ∠C. Therefore, because of ASA.

 

As such, for this course, you should not use AAS as a condition of congruency. Instead, you need to find the third angle and use ASA as a condition of congruency.

 

 

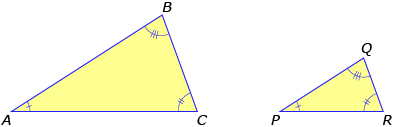
You also showed that not all combinations of measurements will guarantee that two congruent triangles will be produced from the given information.

• AAA: When given three angle measurements, triangles of the same shape but different sizes can be created. These triangles are similar but not necessarily congruent. So, AAA does not provide enough information on its own to guarantee that two triangles are congruent.
  
  

• SSA: More than one triangle can be constructed when given the length of two sides and a non-included angle. So on its own, SSA is not enough information to guarantee congruency.