Lesson 10

Lesson 10 Summary

 

If a design is based on congruent triangles, it is crucial that all the triangles in the design are in fact congruent (the same). If they are not the same, the overall design can be negatively affected. There is a minimum set of angle and side measurements that can be given to ensure that the triangles constructed are the same. To establish congruency, a minimum of three sets of measurements is required:

• SAS (side-angle-side): If two pairs of corresponding sides are equal in length, and the included angles are equal in measure, then the triangles are congruent.

• SSS (side-side-side): If three pairs of corresponding sides are equal in length, then the triangles are congruent.

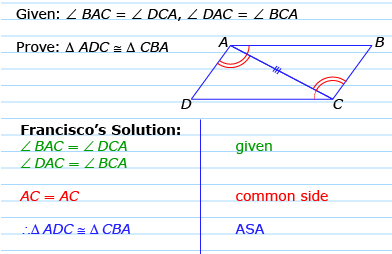
• ASA (angle-side-angle): If two pairs of corresponding angles are equal in measure and the included sides are equal in length, then the triangles are congruent. If two pairs of corresponding angles are equal in measure and a pair of opposite sides is equal in length AAS (angle-angle-side), you need to find the third angle and use ASA as a condition of congruency.

These sets of angle and side measurements can be used to prove that triangles are congruent. Deductive reasoning can also be used to prove the classification of triangles or to prove that parts of triangles are equal. Solving these problems requires first proving that the triangles are congruent.

 

In order for proofs to be valid and understood by others, statements and justifications must be presented in a logical and clear manner. Any errors or unclear steps will result in an invalid proof.

 

In the final lesson in this module, Lesson 11, you will apply your knowledge of the properties of angles to polygons and then analyze and create your own design.