Lesson 11

1. Lesson 11

1.4. Explore

Module 2: Lesson 11

Module 2: Logic and Geometry

Explore

You proved in a previous lesson that the sum of the interior angles of any triangle is 180°.

In Discover you determined the sum of the interior angles of quadrilaterals, pentagons, and hexagons by seeing how many triangles could be drawn in each type of polygon. The sum of the measures of the interior angles of a polygon will equal the sum of the measures of the interior angles of the triangles it contains when one vertex is joined to all of the other vertices.

For example, two triangles can be drawn within a rectangle, so the sum of the interior angles in a rectangle is 2(180°) or 360°.

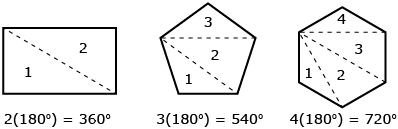
This illustration is a rectangle, a pentagon, and a hexagon that are divided into triangles.

The number of triangles that can be drawn within each type of polygon by connecting one vertex to all of the other vertices is two less than the number of sides in the polygon, or n – 2. Using inductive reasoning, you developed a conjecture about the relationship between the number of sides in a polygon and the sum of the interior angles in a polygon.

This illustration is a computer screen with the words: My conjecture: The sum of the interior angles in a polygon S<img class=

, is S

= 180 degrees (n − 2) where n equals the number of sides in a polygon." width="392" height="362" />

iStockphoto/Thinkstock

Read “Example 1: Reasoning about the sum of the interior angles of a polygon” on page 96 of your textbook to see how deductive reasoning can be used to prove that the sum of the measures of the interior angles of a convex polygon can be expressed as S(n) = 180°(n − 2).

Self-Check 2

Complete “Your Turn” on page 96 of your textbook. Answer

Polygons are also used in many structures in nature. For instance, honeybees store their honey in honeycombs shaped like regular hexagons. Honeycombs are just one example of tessellations that can be found in nature. Recall that tessellations are arrangements of figures on a plane that completely cover a surface without gaps or overlapping.

Amaya is helping her younger brother with his science homework where he is learning about honeybees. Amaya wonders why honeycombs are shaped like hexagons. What makes the six-sided structure work better than another polygon like a pentagon? Would a pentagon even be able to tessellate? She decides to compare the angles in a hexagon and a pentagon to help answer her questions.

Watch the animation Honeycombs to see Amaya’s comparison of pentagons and hexagons.

Amaya was able to apply her knowledge of angles in polygons to help her understand a design in nature. Now it is your turn.