Print this chapterPrint this chapter

Lesson 1

1. Lesson 1

1.5. Discover 2

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

 

function: a relation where each input value has only one output value

A function is a relation where each input value corresponds to only one output value. There are several strategies you can use to determine whether a relation is a function. For instance, you can look at the ordered pairs to see if there is exactly one output value for each input value or you can perform a vertical line test on the graph of the relation. Recall that a graph represents a function if a vertical line cuts the graph only once.

 

tip

Functions are to relations what quads are to all recreational vehicles. In other words, functions are a subset or special type of relation.

 

A graphic shows two labelled boxes: one box is titled Relations and is made up of functions and non-functions. The other box is titled Recreational Vehicles and is comprised of quads and non-quads.



In the following examples, the relationship on the left is a function, whereas the relationship on the right is not. In the latter case, the vertical line crosses the parabola more than once showing that there is more than one output (y) value for some of the input (x) values.

 

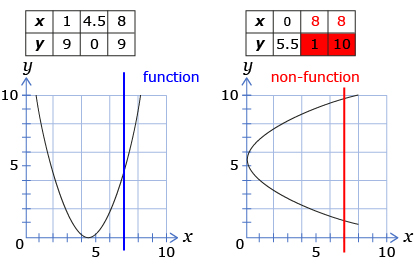
The left graph shows a parabola opening upward and a vertical line that passes through exactly one point on the parabola. The right graph shows a parabola opening to the right and a vertical line passing through two points on the parabola.

 


caution

If you do not remember how to determine whether or not a relation is a function, go to the Refresher section of this lesson and watch Introduction to Functions. It is important that you are comfortable determining whether or not a relation is a function when you are given ordered pairs or a graph of the relation.

 

Share 1
 

With an appropriate partner, compare quadratic and linear relationships. (How are they the same? How are they different?)

 

In your discussion, consider the following:

  • List real-life examples that are described by linear or quadratic relationships.
  • Describe a linear relationship.
  • Describe a quadratic relationship.
  • Describe the graphs of these relationships.
  • Explain how you can tell whether a graph represents a function or a non-function.
  • Describe patterns created by linear relationships.
  • Explain how these differ from patterns created by quadratic relationships.