Print this chapterPrint this chapter

Lesson 1

1. Lesson 1

1.7. Explore

Mathematics 20-2 M3 Lesson 1

Module 3: Quadratics

 
Explore
 

This shows a parabolic grid with Earth in the background.

Comstock/Thinkstock

The shape of the graph of a quadratic relation is called a parabola. In the photo, the thickest blue line could also be described as having a parabolic shape. Can you see the similarity between it and the graphs of the quadratic relations you have observed so far in this lesson?

 

In Try This 1 you discovered how changing the coefficients and constant in a quadratic function written in standard form (y = ax2 + bx + c) can affect the graph of the function. You might have noticed the connection between a and the parabola’s direction:

  • When a is positive, the parabolic graph open upwards.
  • When a is negative, the graph will open downwards.

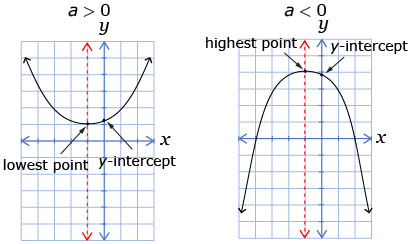
The image on the left shows a parabola opening upwards when a is greater than zero. The lowest point on the parabola is indicated as well as the y-intercept. The image on the right shows a parabola that opens downwards when a is less than zero. The highest point on the parabola is indicated as well as the y-intercept.

from: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 323. Reproduced by permission.



Did you notice how changing the value of b changes the location of the parabola’s line of symmetry and that the highest or lowest point on the parabola lies on the vertical line of symmetry? When you left a and b constant and changed the value of c, did you determine that c is actually the value of the parabola’s y-intercept?

 

You also might have noticed the connection between the value of a and the shape of the graph, specifically the steepness of the opening of the parabola. Changing the value of only a (i.e., b and c are constant) changes the shape of the parabola; however, when you change the value of only b or only c, the shape of the parabola stays the same. Changing only b or only c translates the parabola horizontally or vertically, but the shape of the parabola remains the same.