Module 5

1. Module 5

1.28. Page 3

Mathematics 10-3 Module 5 Lesson 6

Module 5: Angles

Explore

In this activity you will review the relationships between co-interior and co-exterior angles formed when two parallel lines are intersected by a third line.

Try This

Step 1: Draw a line on a blank sheet of paper. This line will serve as the transversal.

This illustration shows a red line segment drawn on a piece of paper.

Step 2: On a second sheet of paper, draw a pair of adjacent supplementary angles similar to the angles shown here.

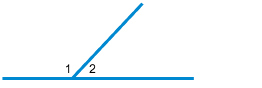
This illustration represents a pair of supplementary angles drawn in blue. The angles are labelled 1 and 2.

Do you remember why ∠1 and ∠2 are supplementary?

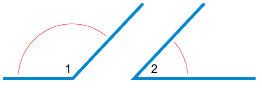
Step 3: Cut out ∠1 and ∠2 along the arms of the angles as shown.

This illustration represents a pair of supplementary angles drawn in blue and labelled 1 and 2. The angles are cut out to become two separate pieces.

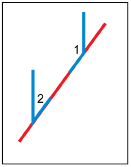
Step 4: Position the angles along one side of the transversal, so that each angle has an arm that touches the transversal and the other two arms of the angles are parallel.

This illustration represents a pair of cut-out supplementary angles drawn in blue placed on a red transversal. One arm of each angle runs along the transversal. The other arms of the angles are parallel.

Self-Check

SC 6. How many different ways can you arrange the angles you cut out to form parallel lines? Draw a diagram for each arrangement. For each arrangement, use the correct term you encountered in the previous lesson to describe each angle pair. For example, to describe the angle pair shown in Step 4, you could use the term co-interior.

Compare your answer.

∠1 and ∠2 are supplementary because they add up to 180°, which is evident because the angles form a straight line.