Print this chapterPrint this chapter

Module 6

1. Module 6

1.4. Page 4

Mathematics 10-3 Module 6 Lesson 1

Module 6: Triangles and Other Polygons

 

Bringing Ideas Together

 

In the Explore section, you investigated similar polygons by changing the grid size upon which the polygons were drawn. You discovered that for those polygons, the corresponding angles were congruent—equal in measure. You also observed that the ratios of the corresponding sides are all equal and determined by the scale factor. Now it is time to see how these similar polygon relationships can be useful in solving problems.

 

Example 1

 

Jasmine is designing a rectangular patio for her neighbour. She has shown her neighbour two sketches. The sketches ABCD and are similar in shape but differ in size.

 

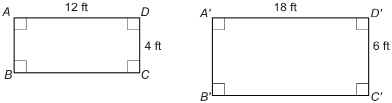
This illustration shows two rectangles. Rectangle ABCD has side AD labelled 12 ft and side CD labelled 4 ft. Rectangle A'B'C'D' has side A'D' labelled 18 ft and side C'D' labelled 6 ft.

  1. Are the corresponding angles congruent?
  2. Determine the ratios of the lengths of the corresponding sides. Are the ratios equal?
  3. What scale factor did Jasmine use to draw
  4. How are the answers to question parts b and c related?

Solution

  1. All angles in the rectangles are right angles and are equal in measure.

     

     


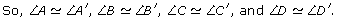
    The corresponding angles are congruent.

  2. Note: Use AB as the symbol for the length of side AB.

     

     



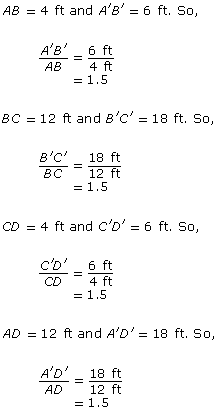
    All the ratios are equal to 1.5.

  3. Jasmine used the scale factor 1.5 to draw 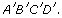She multiplied both the length and width of ABCD by 1.5 to draw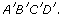 eqn005a.eps

    The length of rectangle ABCD is 12 ft.

    The width of rectangle ABCD is 4 ft.

  4. The scale factor is equal to the ratios of the corresponding sides of the similar figures.
Proportional Reasoning

 

In the previous example, the ratios of corresponding sides are equal.

 

proportion: a statement showing two ratios are equal

 

If the ratios of the sides of two polygons are equal, the sides of the two polygons are said to be proportional.

 

In the next example and in the follow-up question in the Lesson 1 Assignment, you will investigate another method of drawing similar polygons. You will also determine if the sides are proportional and if the corresponding angles are congruent—equal in measure.

 

You will need two sheets of blank paper, two elastic bands, tape, a ruler, a protractor, and your calculator. Work with a partner, if possible.

 

Example 2

 

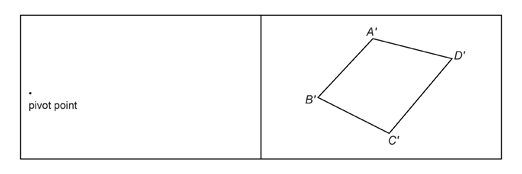
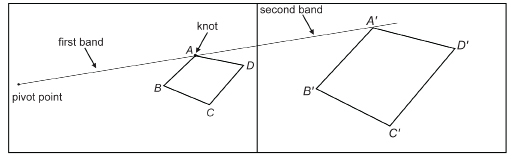
Use two elastic bands to draw a figure similar to quadrilateral ABCD.

 

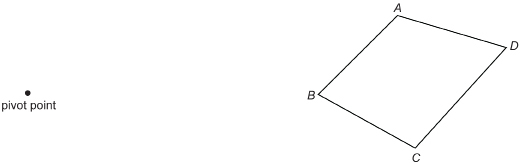
This illustration shows quadrilateral ABCD at the right of a page with a pivot point at the left side of the page.

 

Or you can print “Quad ABCD Diagram” for a copy of the quadrilateral ABCD and pivot point shown above.

 

Solution

 

Step 1: Tape the diagram you printed and a blank sheet of paper beside each other, as shown, on the top of a desk or table. Use masking tape so you do not damage the surface of the table or desk.

 

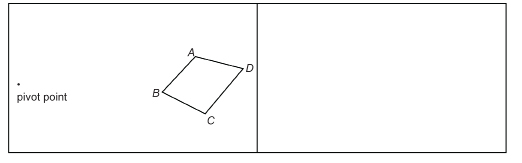
This illustration shows quadrilateral ABCD at the right of one page of paper with a pivot point at the left side of the page. A second page of paper is shown to the right of the original page.

 

Step 2: Tie two elastic bands together. If the bands are the same size, each must be shorter than the distance from the pivot point to the nearest point on ABCD. If the elastics are different sizes, one must be shorter than the distance from the pivot to ABCD.

 

This illustration shows two similarly sized rubber bands tied together. The bands are labelled first band and second band. A knot is labelled between the two bands.

 

 

Step 3: If you are working with a partner, have your partner hold the end of one elastic band on the pivot point. One method is to ask your partner to insert a pen in the loop of that band and place the tip of the pen on the pivot point. Place the tip of your pen in the other loop and stretch the bands so that the knot is on point A. Mark the point on the second sheet where your pen tip is. Call that point, point In a similar fashion, locate points on the second sheet. Join the four points to form

 

This illustration shows two pages of paper taped together with a pivot point at the left, quadrilateral ABCD at the right of the left sheet of paper, and quadrilateral A'B'C'D' on the right sheet of paper. The tied elastic bands are shown with one end fixed at the pivot point, the knot at point A, and the end of the second band on point A'.

 

 

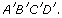
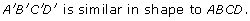
Save your work in the course folder. You will need your work to answer questions from this example in the Lesson 1 Assignment.

 

Mastering Concepts

 

Suppose you wanted to draw a polygon similar to, but smaller than, a given polygon. How might you use the elastic bands?

 

Compare your answer.

Consider a quadrilateral ABCD placed on the right-hand sheet and the pivot point on the left-hand sheet.

 

This illustration shows two sheets of paper taped together with a pivot point on the left of the left sheet, and a quadrilateral ABCD covering most of the right sheet of paper.