Print this chapterPrint this chapter

Module 7

1. Module 7

1.27. Page 5

Mathematics 10-3 Module 7 Lesson 5

Module 7: Trigonometry

 

Working with the Cosine Ratio

 

In the next example you will apply your calculator skills to help you solve a problem involving the cosine ratio. There is not much difference between applying the cosine ratio and applying the sine ratio. All you have to remember is that, for the cosine ratio, the adjacent side is used rather than the opposite side.

 

Example 3

 

This photograph is of a woman painting the side of a house. She is standing on a ladder.

© EML/shutterstock

Angela is painting the exterior of her house. On one side, there is a 5-ft-wide flower garden along the wall. Angela does not want to place the foot of the ladder on her flowers. However, for safety, the ladder must be positioned at a 75° angle with the ground. The ladder is 15 ft in length. Can Angela avoid damaging her flowers if she places the ladder at the correct angle?

 

Solution

 

Draw a diagram.

 

Let x be the distance the foot of the ladder is away from the wall when the ladder leans at 75° to the ground.

 

 

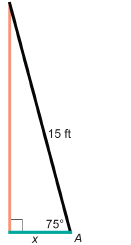
This illustration shows a right triangle with angle A between one of the legs and the hypotenuse measuring 75 degrees. The side opposite angle A is drawn in orange, and the side adjacent is drawn in blue. The adjacent side has a length of x. The hypotenuse has a length of 15 feet.

 

Substitute into the formula.

 

 

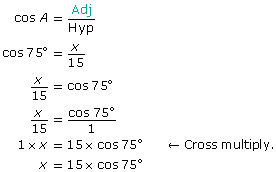
eqn139.eps

 

To calculate x, press these keys.

 

 

This illustration shows the keystrokes needed to find 15 times cosine 75 degrees on a calculator. The keys are shown in this order 1, 5, cos, 7, 5, right parenthesis, and the equal sign.

 

 

 

The foot of the ladder must be 3.9 m from the wall. Angela will not be able to avoid her flowers. However, with a longer ladder she could avoid the flowers.

 

Self-Check

 

Use the method outlined in Example 3 to solve this question.

 

SC 8. Solve for x. Round to two decimal places.

 

 

This illustration shows a right triangle with angle A and a measure of 31 degrees between one leg and the hypotenuse. The side opposite angle A is drawn in orange, and the side adjacent to angle A is drawn in green. The adjacent side measures 5.43 centimetres. The hypotenuse has length x.

 

Compare your answer.

 

Another Angle

 

You have just seen how an unknown side in a right triangle can be determined using the cosine ratio. You found the cosine ratio from the given measure of an angle. But can you go in the other direction? Can you find the measure of an angle from the cosine ratio?

 

For instance, suppose you were told that the cosine of an angle in a right triangle is 0.8. What would that angle be?

 

Example 4

 

If cos A = 0.8, determine ∠A to the nearest degree.

 

View the animated “Cosine Solution.”

 

Self-Check

 

Practise finding angles given the cosine ratio.

 

SC 9. Find ∠A given cos A = 0.6.

 

To find the angle, use both methods shown in Example 4.

 

SC 10. Use your calculator to find each angle from its cosine. Round your answers to the nearest tenth.

 

sin A

∠A

0.1257

 

0.7826

 

0.9000

 

 

 

 

SC 11. Find ∠A to the nearest tenth of a degree.

 

 

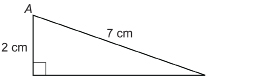
This illustration shows a right triangle with one leg 2 centimetres long and the hypotenuse 7 centimetres long. The angle between these two sides is labelled A.

 

Compare your answers.

 

Mastering Concepts

 

Try this question. When you are finished, check your answer.

 

MC 1. ΔPQR is a right triangle.

 

 

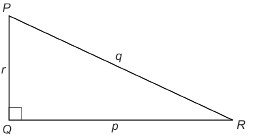
This illustration shows right triangle PQR with angle Q as the right angle. The side opposite angle P is labelled with a lowercase p, the side opposite angle R is labelled with a lowercase r, and the side opposite angle Q is labelled with a lowercase q.

  1. For ΔPQR, write the ratios for sin P, cos P, sin R, and cos R.
  2. How are these ratios related?
  3. How are ∠P and ∠R related?

Compare your answers.