Print this chapterPrint this chapter

Module 7

1. Module 7

1.31. Page 3

Mathematics 10-3 Module 7 Lesson 6

Module 7: Lesson 6

 

Bringing Ideas Together

 

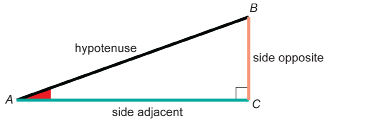
In Explore you checked indirect measurement and the cosine ratio. You used the following relationship to find the angle between the adjacent side (the wall) and the hypotenuse (the diagonal).

 

 

This illustration shows a right triangle with the side opposite angle A in orange, the side adjacent to angle A in green, and the hypotenuse in black. The reference angle is shown in red.

 

 

 

As you did in Explore, this relationship can be used to find an angle. This relationship can also be used in a variety of problem situations to determine the hypotenuse or the adjacent side if you are given the angle and one of these two sides. Study the following examples.

 

Example 1

This is a photo of a radio transmission tower.

Photo copyright SFU Museum of Archaeology & Ethnology. Used with permission.

 

A radio transmission tower is supported by a series of guy wires. One such wire is attached to the ground 10 m away from the foot of the tower. How long is the guy wire if it makes a 50° angle with the ground? Round to one decimal place.

 

View the animated “Guy Wire Solution.”

 

Did You Know?

 

The ancient Greeks used the word theamata instead of the word wonders. Theamata means “things to be seen.” Like the Mayan pyramids or the Inca city of Machu Pichu, the pyramids are one of the world’s wonders to be seen!

 

 

 

 

 

 

 

 

This is a photo of a pyramid.

© Maksym Gorpenyuk/shutterstock

Example 2

 

The Great Pyramid of Khufu at Giza was built more than 4500 years ago. Of the seven wonders of the ancient world, this pyramid is the only one still standing. It stands on a square base with a side length of approximately 230 m. The shortest distance from the apex of the pyramid to the ground along a slanted face of the pyramid is 186 m. That is, the slant height of the pyramid as measured along the middle of a face is 186 m. At what angle is the slant face inclined to the horizontal? Round to the nearest tenth of a degree.

 



Solution

 

Draw a diagram.

 

 

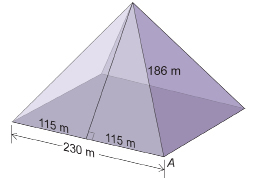
This illustration shows a pyramid with its cross section as an isosceles triangle. The base of this isosceles triangle is shown as having a length of 230 metres. This isosceles triangle is divided into two congruent right triangles. One of these right triangles is labelled with reference angle A, with a side adjacent to angle A of 115 m and a hypotenuse of 186 m.

 

The cross-sectional view of the pyramid can be split into two right triangles, each with a base of 115 m. The base of the pyramid = 2 × base of each right triangle; 230 m = 2 × 115 m.

 

Let ∠A be the angle of elevation.

 

Substitute into the formula.

 

 

 

The slant side is inclined at 51.8° to the horizontal.

 

Example 3

This illustration shows a conical pile of sand and a right triangle in its interior. The right triangle has its hypotenuse along the slope of the conical pile. The vertical side of the right triangle is along the central axis of the conical pile. The horizontal side of the right triangle runs along the ground directly underneath the conical pile from the pile’s edge to a point directly under the top of the pile.

© vita khorzhevska/shutterstock

 

A conical pile of dry sand has a slant side 2 m in length. If the angle the conical surface makes with the ground is 31°, what is the radius of the pile? Round to one decimal place.

 

Solution

 

Draw a diagram.

 

 

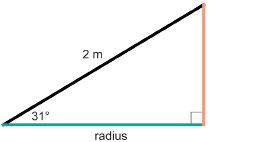
This illustration shows a triangle with a hypotenuse two metres long at an angle of 31 degrees from the horizontal.

 

Let x be the length of the radius.

 

Substitute into the formula.

 

 

 

The radius of the sand pile is approximately 1.7 m.

 

It is your turn to practise these skills!