Print this chapterPrint this chapter

Lesson 3

1. Lesson 3

1.5. Explore

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

Explore

 

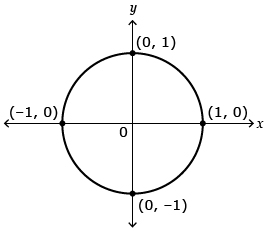
In Try This 1 you took a circle and divided it into sections that were multiples of  and You may have determined that the radius of the circle you made is 1 unit, since the distance around the circle, or the circumference, was 2π.

 

 


 

This is a sketch of a unit circle. The centre is at the origin and the points 1, 0; 0, 1; negative 1, 0; and 0, negative 1 are labelled on the circle.

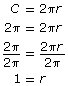
Source: Adapted from Pre-Calculus 12. Whitby, ON: McGraw-Hill

Ryerson, 2011. Reproduced with permission.

A circle with a radius of 1 and the centre at the origin can be called a unit circle.

 

Now that you have found some values for points on a unit circle, you can derive an equation to represent all points on a unit circle. You will use the Pythagorean theorem.

 

Try This 2

 

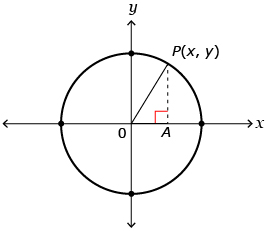
Step 1: Draw a unit circle on an x- and y-axis. This means that you will draw a circle with a radius of 1 and the centre of the circle at the origin (0, 0).

 

Step 2: Label the centre of the circle O.

 

Step 3: Pick any point in quadrant 1 of the unit circle. Label the point P(x, y).

 

Step 4: Draw a line from point O to point P. What is the length of this line segment?

 

Step 5: Label OP on the diagram.

Step 6: Create a right-angle triangle by drawing a vertical line from point P to the x-axis. Label the point on the x-axis A.

  1. What is the length of line segment PA? Label this length.
  2. What is the length of line segment OA? Label this length.
  3. Since this is a right-angle triangle, use the Pythagorean theorem to write an equation that relates the lengths of OP, PA, and OA.

course folder Save your responses in your course folder.

 

Share 2

 

With a partner or in a group, discuss the following questions.

  1. Share the equation you wrote in Try This 2 question 3.
  2. Would your equation change if you chose a different point P?
  3. What would happen if point P were in quadrant 3? Would this change the lengths of PA and OA?

 course folder If required, save a record of your discussion in your course folder.

This will not be a number. Instead, a variable from the coordinate P(x, y) will describe this length.
This will not be a number. Instead, a variable from the coordinate P(x, y) will describe this length.

Your diagram should look something like this:

 

 

This is a diagram of a circle with its centre at the origin and point P(x, y) labelled in quadrant 1. A vertical line is drawn from P to the x-axis. The line is perpendicular to the x-axis.

Source: Pre-Calculus 12. Whitby, ON: McGraw-Hill
Ryerson, 2011. Reproduced with permission.

This is the radius of the circle.