Print this chapterPrint this chapter

Lesson 2

1. Lesson 2

1.6. Explore 2

Mathematics 30-1 Module 5

Module 5: Trigonometry Applications and Identities

 

In Try This 2 you will explore the model of a system that includes numbers.

 

Try This 2

 

A tide chart predicts the height of water at a specific location at particular times. Consider the following tide chart for Vancouver from October 7 to 11, 2011.

 

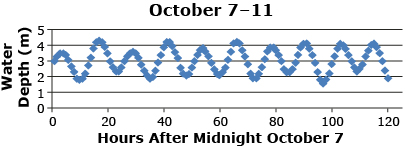
This graph shows the hourly depth of water over time near Vancouver. It oscillates between approximately 1.5 m and 4.5 m.

SOURCE: Tide, Currents, and Water Levels, (Fisheries and Oceans Canada, 2011), <http://www.tides.gc.ca/>; (09/02/2012).

  1. What general shape is the graph? Is a sine or cosine model reasonable?
  2. Try to model the graph using the equation 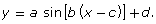Use the following table to help you.

    Graph Dimension What does the dimension represent in the problem? Value of Parameter
    amplitude ≈   a ≈
    period ≈   b ≈
    phase shift ≈   c ≈
    midline ≈   d ≈

    Write your equation in the form

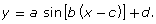
  3. Use Tides Exploration 1 to determine an equation that matches the data. Adjust the parameters a, b, c, and d until the graph overlaps the points as closely as possible. Write down your equation.

     
    This play button opens Tides Exploration 1.

  4. How does the equation you determined in question 2 compare to the equation you determined in question 3?

  5. Three points on the original scatter plot are (10, 1.9), (50, 3.0), and (100, 3.3). Calculate the y-value at the times of 10, 50, and 100 hours by using each of your equations. Use a chart similar to the following one to organize the calculations. How close are your predicted heights to the actual heights?

    x-Value y-Value Using Equation Found in Question 2 y-Value Using Equation Found in Question 3 Actual y-Value
    10     1.9
    50     3.0
    100     3.3
  6. Consider the tide table for the same location from November 16 to 20, 2011. What characteristics of this graph are similar to a sine graph? What is different?

     
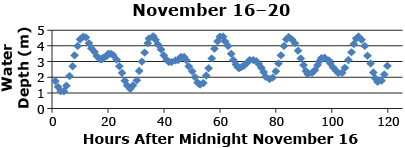
    This graph shows the hourly depth of water over time near Vancouver. It oscillates between approximately 1 m and 5 m.
     
    SOURCE: Tide, Currents, and Water Levels, (Fisheries and Oceans Canada, 2011), <http://www.tides.gc.ca/>; (09/02/2012).
  7. Is it reasonable to use an equation of the form 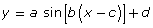to model this data?

  8. Use Tides Exploration 2 in an attempt to model the data using an equation of the form

     

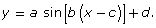
    This play button opens Tides Exploration 2.

  9. Does it make sense to use an equation of the form 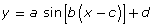to model this data?

course folder Save your answers in your course folder.

 

Share 2

 

With a partner or group, discuss the following questions based on what you learned in Try This 2.

  1. How can you decide when 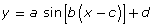should be used to model data?
  2. What advantage is there in using an equation to represent data?
  3. What are some problems with using one of the equations from questions 2 and 3 of Try This 2 to predict the tide height at 5000 h?