Lesson 2

Refresher

 

Simplifying square roots with variables is similar to simplifying square roots with numerical radicands. First, find the prime factorization of the coefficient of the expression. Then, change the entire radical to a mixed radical by treating each variable of the expression as if it were a prime number. You will recall that perfect squares are found when multiplying a number by itself. The same is true for variables. Here are some examples:

 

2 × 2 = 4

 

3 × 3 = 9

 

x × x = x2

 

y2 × y2 = y4

 

It is easy to find the square root of a perfect square. Here are some examples:

 

 

 

 

 

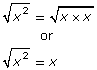
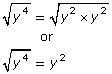
By writing the prime factorization as powers, factors with even exponents can be found quickly and their square roots identified.

 

Remember that there are principal square roots (positive) and secondary square roots (negative). Unless you are asked for both the principal and secondary square roots, the square root sign refers to the principal square root of an expression.

 

Identifying perfect cubes can also help you find cube roots:

 

2 × 2 × 2 = 8

 

3 × 3 × 3 = 27

 

x × x × x = x3

 

y2 × y2 × y2 = y8

 

The cube roots of these expressions are

 

 

 

 

 

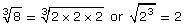
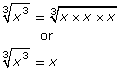
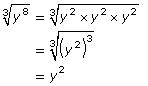
Go back to the Are You Ready? section, and try the questions again. If you are still having difficulty, contact your teacher.