Lesson 2
1. Lesson 2
1.4. Discover
Module 5: Radicals
Discover
iStockphoto/Thinkstock
You already know that you cannot take the square root of a negative number. When you find a square root, you find two numbers that multiply to equal the radicand. For example, to find the square root of 9, find a number that, when multiplied by itself, equals 9.
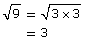
You cannot multiply a number by itself and get a negative answer.
(−3)(−3) = 9
Is it possible to take the cube root of a negative number? What about the fourth root?
Try This 1
Use your calculator to complete Decimal Approximation Chart. You are finding various roots of 2000 and −2000.
There are different ways to find roots, other than square roots, on your calculator. One way is to use a button that allows you to enter the index of a radical. This button often looks like 
The other way is to use an exponent button, usually represented as “^” on calculators. Recall from Mathematics 10C that roots are equivalent to fractional exponents. To find the cube root of a number, raise it to the 
power. For a fourth root, raise it to the 
power, and so on. Be sure to remember to enclose fractions in parentheses. You also need to remember to enclose negative numbers in parentheses, as shown. The keystrokes used are shown.
If your calculator has an “xy” button, put in the number, press the “xy” button, and then put in the appropriate fractional exponent in brackets.
Share 1
Compare your results from Try This 1 with another student or appropriate partner. Once you have come to an agreement on the correct answers, discuss the following questions:
- When is it possible to take the root of a negative number? Describe the patterns you see.
- What rules describe the situation?
Summarize your discussion by creating a general rule about taking the root of a negative number.
Place a copy of your work in your course folder.