Lesson 2

Self-Check 1

 

Complete “Check Your Understanding” question 1 on page 211 of your textbook. Answer

---

In Lesson 1 you learned two methods to convert an entire radical to a mixed radical. You can find the prime factorization or you can find the greatest perfect square factor (or greatest perfect cube when working with cube roots). It doesn’t matter if the expression is made up of numbers or variables, the procedure is the same.

 

You can find the greatest perfect square (or greatest perfect cube) factor of numbers in order to simplify radical expressions:

 

 

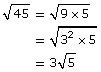
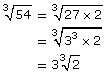
You can find the greatest perfect square (or greatest perfect cube) factor of variables in order to simplify radical expressions:

 

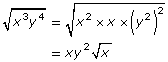
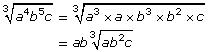
You can find the greatest perfect square (or greatest perfect cube) factor of a combination of both numbers and variables in order to simplify radical expressions:

 

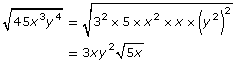
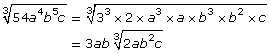
Try This 2

 

Convert to a mixed radical.

1. Write the radicand as a product of two factors, one of which is a perfect square. Be sure to include variables. Answer
   
   
2. Simplify the result by taking the square root of the perfect square out of the radicand. Answer
   
   
3. Use your calculator to verify that the result is equal to 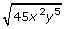by substituting in values for x and y, such as 3 for x and 2 for y. Answer
   
   
4. What other ways could you simplify 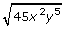? Answer