Print this chapterPrint this chapter

Lesson 6

1. Lesson 6

1.4. Explore 3

Mathematics 30-1 Module 4

Module 4: Foundations of Trigonometry

 

You may have noticed that both y = sin θ and y = cos θ have a period of 2π, or 360°, and both have regular θ-intercepts that are  apart. This pattern continues infinitely for both positive and negative values of θ.

 

Self-Check 2
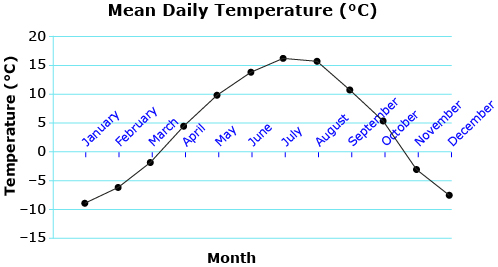
  1. Estimate the period and amplitude of the graph Mean Daily Temperature (°C).

    This is a graph showing the mean daily temperature by month for Calgary.
    Answer

 

textbook

  1. Complete questions 10.a., 10.c., and 14 on pages 234 and 235 of the textbook. Answer


You have begun to see how the graphs of y = sin x and y = cos x are related. Now you will look at transforming these functions.

 

Try This 4

 

A family of functions similar to y = sin x can be represented by the equation y = a sin (bx), where a and b are constants. Use Sine a, b Explorer and Cosine a, b Explorer to investigate how changing these parameters will change the graph of y = sin x and to answer the questions that follow. 


 
This is a play button that opens Sine a, b Explorer.
  1. Record your observations in a table like the one shown as you explore Sine a, b Explorer. Select the check boxes in Sine a, b Explorer to easily see amplitude, period, and the original y = sin x.

      Value of a or b Changes to Graph Sketch Amplitude Period
    Increase a.          
    Decrease a.          
    Return a to 1.  
    Increase b.          
    Decrease b.          


  2. Now use Cosine a, b Explorer to investigate how changing the parameters a and b changes the graph of y = a cos(bx). Record your observations in a table like the one shown.

      Value of a or b Changes to Graph Sketch Amplitude Period
    Increase a.          
    Decrease a.          
    Return a to 1.  
    Increase b.          
    Decrease b.          


     
    This is a play button that opens Cosine a, b Explorer.
  3. Find a numeric relationship between a and the amplitude.
  4. Use your rule to determine the amplitude if a = 27.
  5. Use your rule to determine a if the amplitude is .
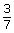  6. Find a numeric relationship between b and the period.
  7. Use your rule to determine the period if b = π.
  8. Use your rule to determine b if the period is 60.

course folder Save your tables and responses in your course folder.

 

Share 3

 

With a partner or in a group, discuss the following questions:
  1. How do the rules that you determined in Try This 4 compare?
  2. How are these rules related to the transformations you learned in Module 1?

course folder If required, save a record of your discussion in your course folder.

You will need to include 2π somewhere in your rule.