Print this chapterPrint this chapter

Lesson 1

1. Lesson 1

1.5. Explore

Mathematics 30-1 Module 5

Module 5: Trigonometry Applications and Identities

 

Explore

 

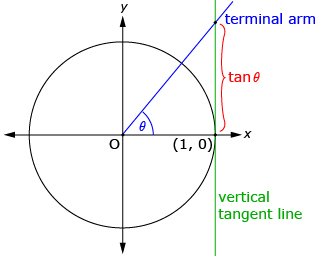
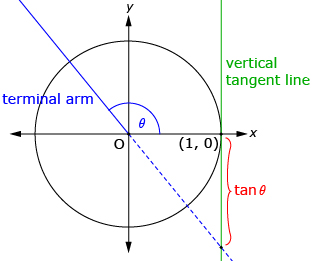
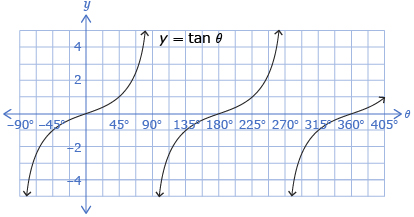
In Try This 1 you plotted the graph of a tangent function that should have looked like the first diagram that follows. The tangent function can be defined as the y-coordinate of the intersection of the terminal arm and a vertical line tangent to the right side of the unit circle as shown in the second and third diagrams.

 

This graph shows f at theta is equal to the tangent of theta where theta is greater than 110 degrees and less than 450 degrees.

 

These diagrams show the terminal arm intersecting a vertical tangent line. The distance from the x-axis to the intersection point is labelled tan theta.

 

When the terminal arm is in quadrant 1 or quadrant 4, the intersection of the terminal arm and the vertical tangent is used to find y.

These diagrams show the terminal arm intersecting a vertical tangent line. The distance from the x-axis to the intersection point is labelled tan theta.

 

When the terminal arm is in quadrant 2 or quadrant 3, an extension of the terminal arm is used to find the intersection with the vertical tangent.

 

In Try This 2 you will explore some characteristics of the tangent function.

 

Try This 2
  1. Using technology, graph the function y = tan x over the domain −4π< x < 4π.
  2. Sketch the graph of y = tan x. Draw in the vertical asymptotes.
  3.  
    1. Determine when tan x = 0.
    2. Write a general equation to represent all the real values of x that make tan x = 0.
  4. The graph of y = tan x is not defined for all x values and includes vertical asymptotes.
    1. At what x values do asymptotes occur?
    2. Write a general equation to represent all the asymptotes of y = tan x over the real numbers.
  5. Determine the period of y = tan x. How does this compare to the period of y = sin x or y = cos x?
  6. Determine the domain and range of y = tan x. How do these sets of values compare to the domain and range of y = sin x or y = cos x?
  7. Determine the amplitude of tan x. What problem do you notice when attempting to determine this amplitude?

course folder Save your answers in your course folder.

Your equation can be of the form x = __ + __ π, n ∈ I.
Your equation can be of the form x = ____ π, n ∈ I.