Lesson 5

Explore

 

When presenting a solution in mathematics, it is best to use an exact value rather than a calculated rounded approximation. This means solutions must often be left in radical form. The reason for this is simple: often when calculating a solution involving radicals, the answer is an irrational number whose decimal will never terminate and never repeat.

 

Fractions with radicals in their denominators are more complex than fractions that do not have a radical in their denominator. As you know in math, answers are given in the simplest form. The simplest form of a fraction would be to eliminate any radicals from the denominator. The process of determining an equivalent fraction that does not have any radicals in the denominator is called rationalizing the denominator.

 

When manipulating a fraction to create a new fraction, it is essential to end up with an equivalent fraction. Be careful that the method removes the radical from the denominator and gives you a fraction that is mathematically equivalent.

 

You learned many years ago that when you multiply any number by 1, you get the original number. You also learned that any number divided by itself is equal to 1.

• 
  
  
• 
  
  
• 
  
  
• 

These principles were introduced when you first learned equivalent fractions.

 

 

It is the same principle that will be applied when you create equivalent fractions by rationalizing the denominator.

 

The quickest way to eliminate a square root sign in the denominator is to multiply the radical by itself, which, of course, will result in the radicand . Remember that since you are working with fractions, whatever you do to the denominator must also be done to the numerator. So instead of multiplying by , you would multiply by .

 

Try This 1

 

The applet Rationalizing Denominators gives a series of steps that make it easy to rationalize the denominator.

 

 

As you saw in the applet, to rationalize the denominator in an expression, multiply both the denominator and the numerator by the expression that will eliminate the radical from the denominator.

 

To rationalize the denominator in , multiply both numerator and denominator by so the denominator is represented as an integer.

 

 

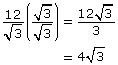
The radical expression is now simplified as far as possible, since there is no radical in the denominator and like terms are collected.

 

Given that , if you had to evaluate the expression without using a calculator, would you rather calculate or ? Why is one preferred over the other if they are equal?