Lesson 3

1. Lesson 3

1.5. Explore 4

Mathematics 30-1 Module 8

Module 8: Permutations, Combinations, and the Binomial Theorem

As with permutations, there are often extra conditions placed on the choices to be made. If, in Self-Check 2, the coach had to make choices based on positions, the number of combinations would change. Consider the scenario in Try This 3.

Try This 3

This photo shows a coach talking with a hockey team.

Ron Chapple Studios/Thinkstock

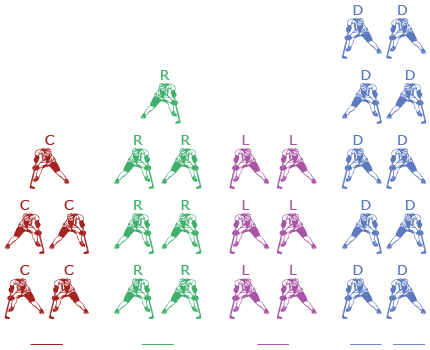
A hockey coach wishes to choose a first line. The coach has to choose 1 of 5 centres, 1 of 7 right wingers, 1 of 6 left wingers, and 2 of 10 defence players. In how many ways can the coach choose the first line?

Use a table similar to the following table to help solve the problem.

Position	Centre	Right Wing	Left Wing	Defence
Number of Players to Choose From	5	7	6	10
Number on Ice at One Time	1	1	1	2
Combination Notation
Number of Ways to Fill Each Position
Total Number of Ways					total = ?

This diagram shows five centres, seven right wingers, six left wingers, and ten defence. At the bottom of the diagram there is a space for a centre, a right winger, a left winger, and ten defense players.

Hemera/Thinkstock

Save your responses in your course folder.

Share 3

With a partner or group, discuss the following questions based on your answer to Try This 3.

Compare the ways your group determined how the starting line could be formed.
Of the methods you saw, describe the one that seems most efficient.

If required, save a record of your discussion in your course folder.

total = 5 × 7 × 6 × 45 = 9450