Lesson 4
1. Lesson 4
1.1. Explore
Module 6: Proportional Reasoning
Explore
proportional: two quantities that are related by a constant ratio
similar objects: two or more 3-D objects that have proportional dimensions
— Source: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 483. Reproduced by permission.
The process of carving a mountain is long and complex. The Crazy Horse Memorial has been in the works since the late 1940s. Before any work on the mountain began, Mr. Ziolkowski created a sculpture of his dream. In order for Crazy Horse to look realistic, Mr. Ziolkowski needed to make sure the sculpture was proportional. In other words, the sculpture’s measurements needed to be proportional to the actual measurements of Crazy Horse and his horse. This means that the model sculptures and the finished memorial are similar objects.
c Ragnar Schierholz /flickr; attribution, non-commercial
scale diagram: a drawing in which measurements are proportionally reduced or enlarged from actual measurements; a scale diagram is similar to the original
enlarge: to increase the dimensions of an image or object by a constant factor
reduce: to decrease the dimensions of an image or object by a constant factor
— Source: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 466. Reproduced by permission.
scale: the ratio of a measurement on a diagram to the corresponding distance measured on the shape or object represented by the diagram
A scale is a ratio or rate, so it always includes units.
— Source: CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 466, 467. Reproduced by permission.
scale factor: a number created from the ratio of any two corresponding measurements of two similar shapes or objects, written as a fraction, a decimal, or a percent
— CANAVAN-MCGRATH ET AL. Principles of Mathematics 11, © 2012 Nelson Education Limited. p. 467, 470. Reproduced by permission.
Scale diagrams of 2-D shapes and scale models of 3-D objects are used to ensure proportionality when an object is enlarged or reduced.
Mr . Ziolkowski created scale models in preparation for carving Crazy Horse into the mountain. When the team started carving Crazy Horse’s head into the mountain, a 60-ft-long measuring boom was used to transfer measurements from a 1:34 scale model to the mountain.
Recently, laser scanning methods have been used to measure the 1:34 and 1:300 scale models. The 1:300 scale model is 
the size of the carving on the mountain, so every aspect of the carving is 300 times larger than the model. In other words, if you lined up 300 of the smaller scale models, their lengths would be the same as the length of the final monument.
Even with technological advancements in surveying, the steps involved in carving the mountain remain the same.
Step 1: Measure the scale model.
Step 2: Measure the mountain.
Step 3: Remove all the rock that doesn’t fit.
To transfer measurements from the scale model to the corresponding section on the mountain, a scale factor needs to be applied.
Scale factors can be used to create larger or smaller versions of an original. When creating the ratio, the first term represents the model or diagram measurement and the second term represents the actual (or object) measurement. A scale factor is a number without units.
The variable k is often used to represent an unknown scale factor.
— CANAVAN-MCGRATH ET AL. Principles of Mathematics 11,
© 2012 Nelson Education Limited. p. 467, 470. Reproduced by permission.
The following formulas are used to calculate scale factor. You may wish to add the following formulas to your Formula Sheet document.
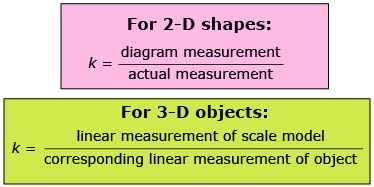
For instance, if measurements are taken off of the 1:300 scale model of Crazy Horse, each measurement would need to be multiplied by a scale factor of 300 to get the corresponding measurement for the mountain monument. This ensures that the mountain carving and the scale model are proportional, or similar objects.